
设向量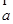 =(1,-3),
=(1,-3), 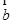 =(-2,4),
=(-2,4), 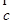 =(-1,-2),若表示向量4
=(-1,-2),若表示向量4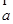 ,4
,4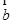 -2
-2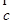 ,2(
,2(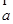 -
-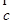 ),
),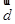 的有向线段首尾相连能构成四边形,则向量
的有向线段首尾相连能构成四边形,则向量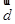 为( )
为( )
| A.(2,6) | B.(-2,6) | C.(2,-6) | D.(-2,-6) |
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com