
某会议室用五盏照明灯,每盏灯各使用灯泡一只,且型号相同.假定每盏灯能否正常照明只与灯泡的寿命有关,该型号的灯泡寿命为
1年以上的概率为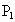 ,寿命为2年以上的概率为
,寿命为2年以上的概率为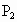 ,从使用之日起每满一年进行一次灯泡更换工作,只更换已坏的灯泡,平时不换.
,从使用之日起每满一年进行一次灯泡更换工作,只更换已坏的灯泡,平时不换.
(1)
在第一次灯泡更换工作中,求不需要更换灯泡的概率和更换两只灯泡的概率.(2)
求在第二次灯泡更换工作中,对其中的某一盏灯来说,该盏灯需要更换灯泡的概率.(3)
当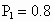 ,
,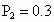 时,求在第二次灯泡更换工作中,至少需要更换4只灯泡的概率(结果保留两位有效数字).
时,求在第二次灯泡更换工作中,至少需要更换4只灯泡的概率(结果保留两位有效数字).  赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com