
分析 利用对数、指数的性质、运算法则求解.
解答 解:log2$\sqrt{\frac{7}{72}}$+log26-$\frac{1}{2}$log228
=$lo{g}_{2}(\sqrt{\frac{7}{72}}×6÷\sqrt{28})$
=$lo{g}_{2}(\frac{1}{12\sqrt{2}}×6)$
=$lo{g}_{2}\frac{1}{2\sqrt{2}}$
=-$\frac{3}{2}$.
0.0081${\;}^{\frac{1}{4}}$-($\frac{27}{8}$)${\;}^{-\frac{2}{3}}$+$\sqrt{3}$•$\root{3}{\frac{3}{2}}$•$\root{6}{12}$
=[(0.3)4]${\;}^{\frac{1}{4}}$-[($\frac{3}{2}$)3]${\;}^{-\frac{2}{3}}$+${3}^{\frac{1}{2}}•\frac{{3}^{\frac{1}{3}}}{{2}^{\frac{1}{3}}}•{3}^{\frac{1}{6}}•{2}^{\frac{1}{3}}$
=0.3-$\frac{4}{9}$+3
=$\frac{257}{90}$.
故答案为:$-\frac{3}{2},\frac{257}{90}$.
点评 本题考查对数式、指数式化简求值,是基础题,解题时要认真审题,注意对数、指数的性质、运算法则的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5,2 | B. | 16,2 | C. | 16,18 | D. | 16,9 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
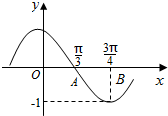
| A. | $y=sin(-\frac{5}{6}x+\frac{3π}{5})$ | B. | $y=sin(\frac{6}{5}x-\frac{2π}{5})$ | C. | $y=sin(\frac{6}{5}x+\frac{3π}{5})$ | D. | $y=-cos(\frac{5}{6}x+\frac{3π}{5})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({\frac{1}{2},1})$ | B. | $({\frac{1}{2},+∞})$ | C. | $({0,\frac{1}{2}}]∪[{1,+∞})$ | D. | $({0,\frac{1}{2}})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com