练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】下列命题中，正确的是( )
    A.斜率相等的两条直线一定平行
    B.若两条不重合的直线l1 ， l2平行，则它们的斜率一定相等
    C.直线l1：x＝1与直线l2：x＝2不平行
    D.直线l1：( －1)x＋y＝2与直线l2：x＋( ＋1)y＝3平行

    【答案】D
    【解析】A错误，斜率相等的两条直线还可能重合．B错误，当两条不重合的直线l1，l2平行时，它们的斜率可能相等，也可能不存在．C错误，直线l1与l2的斜率都不存在，且1≠2，所以两直线平行．D正确，由于直线l1：( －1)x＋y＝2与直线l2：x＋( ＋1)y＝3的斜率分别为k1＝1－ ，k2＝－ ＝1－ ，则k1＝k2，所以l1∥l2.

    故答案为：D

    根据两条直线平行以及垂直的斜率的关系逐一判断即可得出结论。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】若cosα=﹣ ，α是第三象限的角，则
    （1）求sin（α+ ）的值；
    （2）求tan2α

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线l在x轴上的截距比在y轴上的截距大1，且过点(6，-2)，求直线l的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】
    （1）已知点M(1，-3)，N(1，2)，P(5，y)，且∠NMP=90°，则log8(7+y)=.
    （2）若把本题中“∠NMP=90°”改为“log8(7+y)= ”，其他条件不变，则∠NMP=.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知四棱锥P﹣ABCD中PA⊥平面ABCD，且PA=4PQ=4，底面为直角梯形， ∠CDA=∠BAD=90°， ，M，N分别是PD，PB的中点．

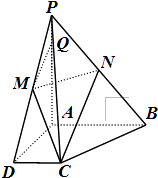
    （1）求证：MQ∥平面PCB；
    （2）求截面MCN与底面ABCD所成二面角的大小；
    （3）求点A到平面MCN的距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知直线l的倾斜角为135°，直线l1经过点A(3,2)，B(a ， －1)，且l1与l垂直，直线l2：2x＋by＋1＝0与直线l1平行，则a＋b等于( )
    A.－4
    B.－2
    C.0
    D.2

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥P﹣ABCD中，PA⊥底面ABCD，AB⊥AD，AC⊥CD，∠ABC=60°，PA=AB=BC，E是PC的中点．求证：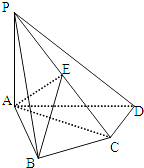

    （Ⅰ）CD⊥AE；
    （Ⅱ）PD⊥平面ABE．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在 中， ， ，点 在 边上，且 ， ．

    （I）求 ；
    （II）求 的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某工厂对一批产品进行了抽样检测．右图是根据抽样检测后的（产品净重，单位：克）数据绘制的频率分布直方图，其中产品净重的范围是[96，106]，样本数据分组为[96，98），[98，100），[100，102），[102，104），[104，106]，已知样本中产品净重小于100克的个数是36，下列命题中：①样本中净重大于或等于98克并且小于102克的产品的个数是60；②样本的众数是101；③样本的中位数是 ； ④样本的平均数是101.3．
    正确命题的代号是（写出所有正确命题的代号）．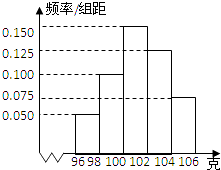

    查看答案和解析>>

    同步练习册答案