练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    17．如图，网格纸上每个正方形小格的边长为1，图中粗线画出的是某多面体的三视图，则该几何体的表面积为（　　）
    A．$56+16\sqrt{2}$B．56+8$\sqrt{2}$C．64D．72

    分析 由三视图可知：该几何体为上下两部分，上面是一个三棱柱，下面是一个长方体．

    解答 解：由三视图可知：该几何体为上下两部分，上面是一个三棱柱，下面是一个长方体．
    ∴该几何体的表面积=2×$\frac{1}{2}×4×2$+$4×2\sqrt{2}$×2+2×4×4+4×4=16$\sqrt{2}$+56．
    故选：A．

    点评 本题考查了三视图的有关计算、三棱柱与长方体的表面积计算公式，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    20．现有16个不同小球，其中红色、黄色、蓝色、绿色小球各4个，从中任取3个，要求这3个小球不能是同一颜色，且红色小球至多1个，不同的取法为472．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

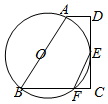    8．已知：如图，梯形ABCD中，AD∥BC，∠C=$\frac{π}{2}$，以AB为直径的⊙O恰与CD相切于点E，⊙O交BC于F，连结EF．
    （Ⅰ）求证：AD+BC=AB；
    （Ⅱ）求证：EF是AD与AB的等比中项．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

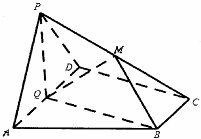    5．如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AD∥BC，AD⊥DC，平面PAD⊥底面ABCD，Q为AD的中点，M是棱PC的中点，PA=PD=2，BC=$\frac{1}{2}$AD=1，CD=$\sqrt{3}$．
    （Ⅰ）求证：PQ⊥AB；
    （Ⅱ）求二面角P-QB-M的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    12．已知直角梯形ABCD中，AB∥CD，∠A=$\frac{π}{2}$，AD=1，AB=2CD=4，E为AB中点，将△ADE沿直线DE折起到△A1DE，使得A1在平面EBCD上的射影H在直线CD上．
    （Ⅰ）求证：平面A1EC⊥平面A1DC；
    （Ⅱ）求平面DEA1与平面A1BC所成的锐二面角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

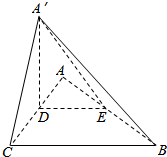    2．如图，△ABC是等腰直角三角形，∠ACB=90°，AC=2a，D，E分别为AC，AB的中点，沿DE将△ADE折起，使得二面角A′-CB-A为45°．
    （Ⅰ）求证：CD⊥A′E；
    （Ⅱ）求平面A′CD与平面A′BE夹角的余弦值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

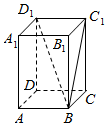    9．在正四棱柱ABCD-A1B1C1D1中，底面边长为1，C1B与底面ABCD所成的角的大小为arctan2，如果平面BD1C1与底面ABCD所成的二面角是锐角，求出此二面角的大小（结果用反三角函数值）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．设函数f（x）=$\sqrt{|x+1|+|x-1|-m}$．
    （1）当m=4时，求函数f（x）的定义域M；
    （2）当a，b∈∁RM时，证明：2|a+b|＜|4+ab|．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    7．若方程x2+mx+n=0（m，n∈R）的解集为{-2，-1}，则m=3，n=2．

    查看答案和解析>>

    同步练习册答案