【答案】
分析:(1)分当a
n∈(0,3]时和当a
n∈(3,6]时,分别求出a
n+1的范围,得到要证的不等式.
(2)当a=1时,利用通项求出a
2=2,a
3=4,a
4=1,得到满足题意的k=3t,t∈N*.同理可得,a取其他值时k的取值,
(3)通过解不等式判断出项的取值范围,从而判断出项之间的关系,选择合适的求和方法求出和.
解答:解:(1)当a
n∈(0,3]时,则a
n+1=2a
n∈(0,6],
当a
n∈(3,6]时,则a
n+1=a
n-3∈(0,3],
故a
n+1∈(0,6],
所以当0<a
n≤6时,总有0<a
n+1≤6. …(5分)
(2)①当a=1时,a
2=2,a
3=4,a
4=1,故满足题意的k=3t,t∈N*.
同理可得,当a=2或4时,满足题意的k=3t,t∈N*.
当a=3或6时,满足题意的k=2t,t∈N*.
②当a=5时,a
2=2,a
3=4,a
4=1,故满足题意的k不存在.
③当a≥7时,由(1)知,满足题意的k不存在.
综上得:当a=1,2,4时,满足题意的k=3t,t∈N*;
当a=3,6时,满足题意的k=2t,t∈N*. …(12分)
(3)由m∈N*,可得2
m-1≥1,故
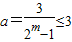
,
当1<k≤m时,
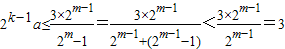
.
故a
k=2
k-1a且a
m+1=2
ma.又
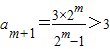
,-------(15分)
所以
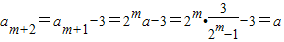
.
故S
4m+2=S
4(m+1)-a
4m+3-a
4m+4=4(a
1+a
2+•…+a
m+1)-(2
m-1+2
m)a
=4(1+2+…+2
m)a-3×2
m-1a=4(2
m+1-1)a-3×2
m-1a
=

. …(18分)
点评:解决睡了的求和问题,关键是求出数列的通项,然后根据数列通项的特点选择合适的求和方法.

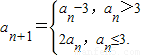
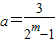 (m∈N﹡),试求数列{an}的前4m+2项的和s4m+2.
(m∈N﹡),试求数列{an}的前4m+2项的和s4m+2.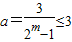 ,
,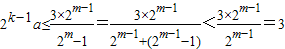 .
.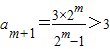 ,-------(15分)
,-------(15分)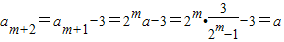 .
. . …(18分)
. …(18分)

 名校课堂系列答案
名校课堂系列答案
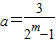 (m∈N﹡),试求数列{an}的前4m+2项的和s4m+2.
(m∈N﹡),试求数列{an}的前4m+2项的和s4m+2.