
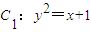 和抛物线
和抛物线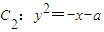 在交点处的两条切线互相垂直,求实数a的值.
在交点处的两条切线互相垂直,求实数a的值. 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:高中数学 来源: 题型:
| ||
| 2 |
| 2 |
| ||
| 2 |
| 24 |
| 25 |
查看答案和解析>>
科目:高中数学 来源:2010届江西省高三年级数学热身卷(文科) 题型:解答题
(12分)已知抛物线 和点M(2,2),若抛物线L上存在不同的两点A、B满足
和点M(2,2),若抛物线L上存在不同的两点A、B满足 。
。
(1)求实数p的取值范围;
(2)当 时,抛物线L上是否存在异于A、B的点C,使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线?若存在,求出点C的坐标;若不存在,请说明理由。
时,抛物线L上是否存在异于A、B的点C,使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线?若存在,求出点C的坐标;若不存在,请说明理由。
查看答案和解析>>
科目:高中数学 来源:2010年北京市海淀区高三第二次模拟考试数学(理) 题型:解答题
(本小题满分13分)
已知椭圆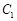 和抛物线
和抛物线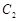 有公共焦点F(1,0),
有公共焦点F(1,0), 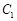 的中心和
的中心和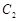 的顶点都在坐标原点,过点M(4,0)的直线
的顶点都在坐标原点,过点M(4,0)的直线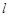 与抛物线
与抛物线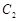 分别相交于A,B两点.
分别相交于A,B两点.
(Ⅰ)写出抛物线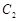 的标准方程;
的标准方程;
(Ⅱ)若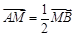 ,求直线
,求直线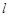 的方程;
的方程;
(Ⅲ)若坐标原点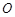 关于直线
关于直线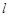 的对称点
的对称点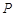 在抛物线
在抛物线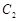 上,直线
上,直线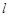 与椭圆
与椭圆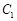 有公共点,求椭圆
有公共点,求椭圆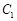 的长轴长的最小值.
的长轴长的最小值.
查看答案和解析>>
科目:高中数学 来源:2010届江西省高三年级数学热身卷(文科) 题型:解答题
(12分)已知抛物线 和点M(2,2),若抛物线L上存在不同的两点A、B满足
和点M(2,2),若抛物线L上存在不同的两点A、B满足 。
。
(1)求实数p的取值范围;
(2)当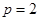 时,抛物线L上是否存在异于A、B的点C,使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线?若存在,求出点C的坐标;若不存在,请说明理由。
时,抛物线L上是否存在异于A、B的点C,使得经过A、B、C三点的圆和抛物线L在点C处有相同的切线?若存在,求出点C的坐标;若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com