
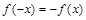 ”的分段函数
”的分段函数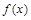 叫做“对偶函数”,已知函数
叫做“对偶函数”,已知函数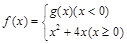 是“对偶函数”,则(1)
是“对偶函数”,则(1) ;
;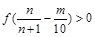 对任意正整数
对任意正整数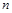 都成立,实数
都成立,实数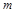 的取值范围为 .
的取值范围为 .科目:高中数学 来源:不详 题型:解答题
 (单位:微克)与时间
(单位:微克)与时间 (单位:小时)之间近似满足如图所示的曲线.
(单位:小时)之间近似满足如图所示的曲线.
 与
与 之间的函数关系式
之间的函数关系式 ;
; 微克时,治疗有效.问:服药多少小时开始有治疗效果?治疗效果能持续多少小时?(精确到0.1)(参考数据:
微克时,治疗有效.问:服药多少小时开始有治疗效果?治疗效果能持续多少小时?(精确到0.1)(参考数据: ).
).查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
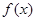 的定义域为
的定义域为 ,若存在闭区间
,若存在闭区间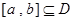 ,使得函数
,使得函数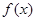 满足:①
满足:①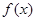 在
在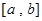 上是单调函数;②
上是单调函数;②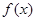 在
在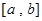 上的值域是
上的值域是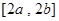 ,则称区间
,则称区间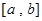 是函数
是函数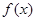 的“和谐区间”.下列结论错误的是( )
的“和谐区间”.下列结论错误的是( )A.函数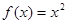 ( (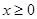 )存在“和谐区间” )存在“和谐区间” |
B.函数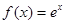 ( (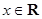 )不存在“和谐区间” )不存在“和谐区间” |
C.函数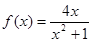 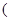 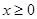 )存在“和谐区间” )存在“和谐区间” |
D.函数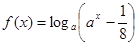 ( (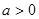 , ,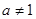 )不存在“和谐区间” )不存在“和谐区间” |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
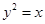 的图象绕远点沿逆时针方向旋转
的图象绕远点沿逆时针方向旋转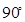 就得到函数
就得到函数 的图象,若把双曲线
的图象,若把双曲线 的图象绕原点逆时针方向旋转一定的角度
的图象绕原点逆时针方向旋转一定的角度 后,就得到某一函数的图象,则旋转角
后,就得到某一函数的图象,则旋转角 可以是( )
可以是( )A. | B. | C. | D.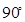 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com