
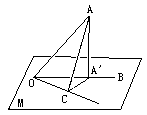
OA是平面M的斜线,O为斜足,OB是OA在平面M内的射影,OC是M内过O的任一直线,设∠AOB=α,∠BOC=β,∠COA=γ.α,β,γ均为锐角.(1)求α,β,γ应满足的关系;(2)指出α,β,γ中的最大角并说明理由.
科目:高中数学 来源: 题型:
| n |
| M |
| AM |
| n |
| n |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com