
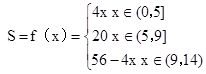 (2)20
(2)20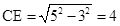 ,∴
,∴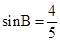
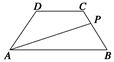
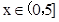 时,过P点作PF⊥AB于F,
时,过P点作PF⊥AB于F,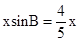 ,∴当
,∴当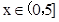 时,
时,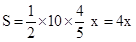
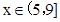 时,
时,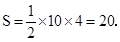
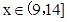 时,
时,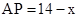
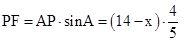
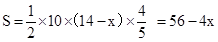 .综上可知,
.综上可知,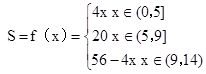
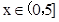 时,f(x)=4x为增函数,
时,f(x)=4x为增函数,

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:高中数学 来源:不详 题型:解答题
 的解析式及其定义域;
的解析式及其定义域;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
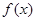 称为“好函数”:对于在
称为“好函数”:对于在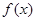 定义域内的任意三个数
定义域内的任意三个数 ,若这三个数能作为三角形的三边长,则
,若这三个数能作为三角形的三边长,则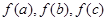 也能作为三角形的三边长.现有如下一些函数:
也能作为三角形的三边长.现有如下一些函数: 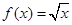 ②
②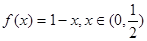
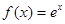 ,
, ④
④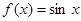 ,
,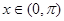 .
.| A.①② | B.①②③ | C.②③④ | D.①③④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com