练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    任意确定四个日期，其中至少有两个是星期天的概率为________．
    记“取到的日期为星期天”为事件A，则P(A)＝，Ai表示取到的四个日期中有i个星期天(i＝0,1,2,3,4)，
    则P(A0)＝C4004＝，
    P(A1)＝C4113＝，
    故至少有两个星期天的概率为
    1－[P(A0)＋P(A1)]＝.
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    设每个工作日甲、乙、丙、丁4人需使用某种设备的概率分别是0.6， 0.5,0.5,0.4，各人是否使用设备相互独立，
    （1）求同一工作日至少3人需使用设备的概率；
    (2)实验室计划购买k台设备供甲、乙、丙、丁使用，若要求“同一工作日需使用设备的人数大于k”的概率小于0.1，求k的最小值.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    为了解心肺疾病是否与年龄相关，现随机抽取了40名市民，得到数据如下表：
     
    		患心肺疾病
    		不患心肺疾病
    		合计
    大于40岁
    		16
    		 
    		 
    小于等于40岁
    		 
    		12

    合计
    		 
    		 
    		40
    已知在全部的40人中随机抽取1人，抽到不患心肺疾病的概率为
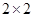    （1）请将列联表补充完整；
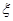    （2）已知大于40岁患心肺疾病市民中，经检查其中有4名重症患者，专家建议重症患者住院治疗，现从这16名患者中选出两名，记需住院治疗的人数为，求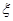的分布列和数学期望；
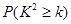    （3）能否在犯错误的概率不超过0.01的前提下认为患心肺疾病与年龄有关？
    下面的临界值表供参考：

    		0.15
    		0.10
    		0.05
    		0.025
    		0.010
    		0.005
    		0.001

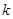    		2.072
    		2.706
    		3.841
    		5.024
    		6.635
    		7.879
    		10.828
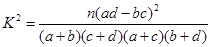    （参考公式：，其中）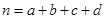

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    栽培甲、乙两种果树，先要培育成苗，然后再进行移栽．已知甲、乙两种果树成苗的概率分别为，，移栽后成活的概率分别为，．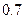
    （1）求甲、乙两种果树至少有一种果树成苗的概率；
    （2）求恰好有一种果树能培育成苗且移栽成活的概率．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    老师要从10篇课文中随机抽3篇让学生背诵，规定至少要背出其中2篇才能及格．某同学只能背诵其中的6篇，试求：
    (1)抽到他能背诵的课文的数量的分布列；
    (2)他能及格的概率．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    某公司有5万元资金用于投资开发项目，如果成功，一年后可获利12%；如果失败，一年后将丧失全部资金的50%.下表是过去200例类似项目开发的实施结果：
    投资成功
    		投资失败
    192例
    		8例
    则该公司一年后估计可获收益的数学期望是________元．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

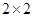    为了研究性别不同的高中学生是否爱好某项运动,运用列联表进行独立性检验,经计算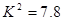,则所得到的统计学结论是:有______的把握认为“爱好该项运动与性别有关”.附:

    		0.050
    		0.010
    		0.001

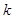    		3.841
    		6.635
    		10.828
     

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    中、日两国争夺某项国际博览会的申办权，进入最后一道程序，由国际展览局三名执委投票，决定承办权的最后归属。资料显示，A，B，C三名执委投票意向如下表所示

    		中 国
    		日 本
    A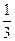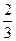


    B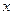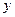


    C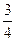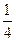


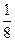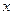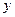    规定每位执委只有一票，且不能弃权，已知中国获得3票的概率为。
    （1）求，的值；
    （2）求中国获得承办权的概率。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知随机变量X的分布列是

    则E(X)和D(X)分别等于(　　)
    A．1和0B．1和1.8C．2和2D．2和0.8

    查看答案和解析>>

    同步练习册答案