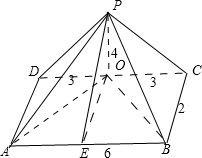
分析:由三视图可知原四棱锥如图所示:底面是一个边长分别为2,6的矩形,侧面PDC⊥底面ABCD,且OP⊥CD,OD=OC=3,OP=4.据此可计算出原几何体的表面积.
解答:解:由三视图可知原四棱锥如图所示:底面是一个边长分别为2,6的矩形,侧面PDC⊥底面ABCD,且OP⊥CD,OD=OC=3,OP=4.
由此可得:PC=
=5,PA=PB=
=
,则等腰△PAB的底边AB上的高=
=2
,∴
S△=×6×2=
6.∵侧面PDC⊥底面ABCD,BC⊥交线CD,∴BC⊥PC,同理AD⊥PD,
∴S
△PCB=S
△PDA=
×2×5=5.
∵OP⊥CD,∴S
△PCD=
×6×4=12.
又S
矩形ABCD=6×2=12.
∴S四棱锥P-ABCD=12+2×5+12+
6=34
+6.
点评:本题考查了由三视图求原几何体的表面积,正确恢复原几何体是解决问题的关键.

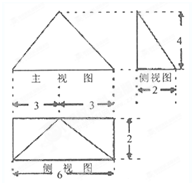 如图是某四棱锥的三视图,求该几何体的表面积.
如图是某四棱锥的三视图,求该几何体的表面积.

