
分析 (1)根据函数奇偶性的性质建立方程关系进行求解即可.
(2)根据函数单调性的定义进行证明.
(3)根据函数奇偶性和单调性的关系将不等式进行转化,利用对数函数的性质解对数不等式即可.
解答 解:(1)∵f(x)=2x+$\frac{m}{{2}^{x}}$(m为常数)为偶函数.
∴f(-1)=f(1),即$\frac{1}{2}$+2m=2+$\frac{m}{2}$,
即$\frac{3}{2}$m=$\frac{3}{2}$,即m=1,
此时f(x)=2x+2-x.为偶函数.
(2)证明:设x1,x2是[0,+∞)任意的两个数且x1<x2,
则$f({x_1})-f({x_2})={2^{x_1}}+{2^{-{x_1}}}-{2^{x_2}}-{2^{-{x_2}}}$
=${2^{x_1}}-{2^{x_2}}+\frac{{{2^{x_2}}-{2^{x_1}}}}{{{2^{x_1}}•{2^{x_2}}}}$
=$({{2^{x_1}}-{2^{x_2}}})({1-\frac{1}{{{2^{x_1}}•{2^{x_2}}}}})$,
∵0≤x1<x2,y=2x是增函数,
∴${2^{x_2}}>{2^{x_1}}>1$;
∴${2^{x_1}}-{2^{x_2}}<0,1-\frac{1}{{{2^{x_1}}•{2^{x_2}}}}>0$;
∴f(x1)-f(x2)<0,
即f(x1)<f(x2),
∴f(x)在[0,+∞)上是单调增函数.
(3)∵f(2)=2+$\frac{1}{2}$=$\frac{5}{2}$,
∴不等式f(logax)>$\frac{5}{2}$等价为f(logax)>f(2),
∵函数f(x)是偶函数,
∴不等式等价为f(|logax|)>f(2),
即|logax|>2,
即logax>2或logax<-2,
若a>1,得x>a2或0<x<$\frac{1}{{a}^{2}}$,
若0<a<1,得0<x<a2或x>$\frac{1}{{a}^{2}}$,
即不等式的解集为当a>1,{x|x>a2或0<x<$\frac{1}{{a}^{2}}$}
当0<a<1,得{x|0<x<a2或x>$\frac{1}{{a}^{2}}$}.
点评 本题主要考查函数奇偶性和单调性的应用和证明,利用函数奇偶性的定义和单调性的定义是解决本题的关键.


 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | (n-2)•2n | B. | 1-$\frac{1}{{2}^{n}}$ | C. | $\frac{2}{3}$(1-$\frac{1}{{4}^{n}}$) | D. | $\frac{2}{3}$(1-$\frac{1}{{2}^{n}}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
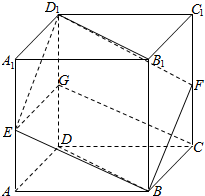 如图,已知E、F、G分别是棱长为2的正方体ABCD-A1B1C1D1的棱AA1、CC1、DD1的中点.
如图,已知E、F、G分别是棱长为2的正方体ABCD-A1B1C1D1的棱AA1、CC1、DD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,-4,2) | B. | (-2,4,-2) | C. | (-2,0,-2) | D. | (2,1,-3) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,2) | B. | (-∞,$\frac{1}{2}$)∪(2,+∞) | C. | ($\frac{1}{2}$,1)∪(2,+∞) | D. | (0,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
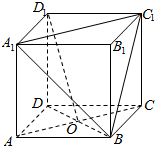 已知正方体ABCD-A1B1C1D1,各棱长为1,O是底面ABCD对角线的交点.
已知正方体ABCD-A1B1C1D1,各棱长为1,O是底面ABCD对角线的交点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com