解:(1)由题意知K(P)中的值有6,8,10,12和14五个值,∴k(P)=5,
K(Q)中的值有6,10,18,12,20,24,∴k(Q)=6
(2)证明:a
i+a
j(1≤i<j≤n)共有
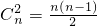
个
所以

下面证明所有a
i+a
j(1≤i<j≤n)各不相同
任取a
i+a
j和a
k+a
l(1≤i<j≤n,1≤k<l≤n)
当j=l时,若a
i+a
j=a
k+a
l,则a
i=a
k,矛盾
当j≠l时,若a
i+a
j=a
k+a
l,则a
i+a
j<2a
j=2
j+1≤a
l<a
k+a
l即a
i+a
j≠a
k+a
l所以所有a
i+a
j(1≤i<j≤n)各不相同,所以
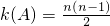
(3)不妨设a
1<a
2<<a
n,
所以a
1+a
2<a
1+a
3<<a
1+a
n<a
2+a
n<<a
n-1+a
n所以a
i+a
j(1≤i<j≤n)中至少有2n-3个不同的数,即k(A)≥2n-3
取A={1,2,3,,n},则a
i+a
j∈{3,4,5,,2n-1}共2n-3个
所以k(A)的最小值2n-3
分析:(1)由题意知k(P)=5,k(Q)=6
(2)a
i+a
j(1≤i<j≤n)共有
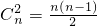
个.所以

.然后利用题设条件证明所有a
i+a
j(1≤i<j≤n)各不相同.
(3)设a
1<a
2<<a
n,所以a
1+a
2<a
1+a
3<…<a
1+a
n<a
2+a
n<…<a
n-1+a
n.由此能够推出k(A)的最小值2n-3.
点评:本题考查集合与元素的位置关系,解题时要认真审题,仔细解答.

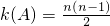 ;
;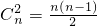 个
个
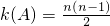
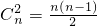 个.所以
个.所以 .然后利用题设条件证明所有ai+aj(1≤i<j≤n)各不相同.
.然后利用题设条件证明所有ai+aj(1≤i<j≤n)各不相同.

 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案