
| a |
| b |
| a |
| b |
| a |
| b |
| AB |
| a |
| CD |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
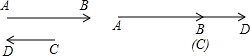
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |


科目:高中数学 来源:“伴你学”新课程 数学·必修3、4(人教B版) 人教B版 题型:022
给出下面命题:
①若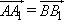 ,则四边形ABB1A1是平行四边形;
,则四边形ABB1A1是平行四边形;
②若三个非零向量a,b,c满足a+b+c=0,则表示它们的有向线段一定能构成三角形;
③对于平面内任一点P,都有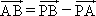 ;
;
④对于任意向量a,b都有|a|+|b|=|a+b|.
其中假(不正确)命题的序号为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年莆田四中一模理)有以下几个命题:
①由![]() 的图象向右平移
的图象向右平移![]() 个单位长度可以得到
个单位长度可以得到![]() 的图象;
的图象;
②若![]() ,则使
,则使![]() 取得最大值和最小值的最优解都有无数多个;
取得最大值和最小值的最优解都有无数多个;
③若![]() 为一平面内两非零向量,则
为一平面内两非零向量,则![]() 是
是![]() 的充要条件;
的充要条件;
④过空间上任意一点有且只有一个平面与两条异面直线都平行。
⑤若椭圆的左、右焦点分别为![]() ,
,![]() 是该椭圆上的任意一点,则点
是该椭圆上的任意一点,则点![]() 关于
关于![]() 的外角平分线的对称点
的外角平分线的对称点![]() 的轨迹是圆。其中真命题的序号为 .(写出所有真命题的序号)
的轨迹是圆。其中真命题的序号为 .(写出所有真命题的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com