
已知定义在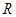 上的函数
上的函数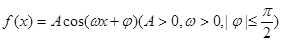 ,最大值与最小值的差为4,相邻两个最低点之间距离为
,最大值与最小值的差为4,相邻两个最低点之间距离为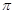 ,函数
,函数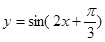 图象所有对称中心都在
图象所有对称中心都在 图象的对称轴上.
图象的对称轴上.
(1)求 的表达式;
的表达式;
(2)若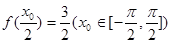 ,求
,求 的值;
的值;
(3)设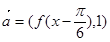 ,
,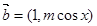 ,
, ,若
,若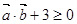 恒成立,求实数
恒成立,求实数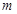 的取值范围.
的取值范围.
(1) (2)
(2) (3)
(3)
【解析】(1)由已知中已知定义在R上的函数f(x)=Acos(ωx+φ)(A>0,ω>0,|φ|≤ ),最大值与最小值的差为4,相邻两个最低点之间距离为π,我们易计算出A值,及最小正周期,进而求出ω值,再由函数
),最大值与最小值的差为4,相邻两个最低点之间距离为π,我们易计算出A值,及最小正周期,进而求出ω值,再由函数 图象所有的对称中心都在y=f(x)图象的对称轴上,求出φ值,即可得到f(x)的表达式;
图象所有的对称中心都在y=f(x)图象的对称轴上,求出φ值,即可得到f(x)的表达式;
(2)由 ,结合(1)中所求的函数解析式,可得
,结合(1)中所求的函数解析式,可得 ,
,
进而求出 的值,然后根据两角差的余弦公式,即可求出答案.
的值,然后根据两角差的余弦公式,即可求出答案.
(3)由  ,
, 恒成立,可以转化为函数恒成立问题,构造函数,求出其最值,即可得到答案.
恒成立,可以转化为函数恒成立问题,构造函数,求出其最值,即可得到答案.
解: (1)依题意可知: ,
,
 与f(x)相差
与f(x)相差 ,即相差
,即相差 ,
,
所以 或
或
 (舍),
(舍),
故 .
……………………4分
.
……………………4分
(2)因为 ,即
,即 ,
,
因为 ,又
,又 ,y=cosx在
,y=cosx在 单调递增,
单调递增,
所以 ,所以
,所以 ,
,
于是
 ………9分
………9分
(3)因为 ,
, ,
,
 ,
,
于是 ,得
,得 对于
对于 恒成立,
恒成立,
因为 ,故
,故 . ………………14分
. ………………14分


 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源:2013-2014学年天津市蓟县高三上学期期中考试文科数学试卷(解析版) 题型:解答题
已知定义在 上的函数
上的函数 ,其中
,其中 为常数.
为常数.
(1)当 是函数
是函数 的一个极值点,求
的一个极值点,求 的值;
的值;
(2)若函数 在区间
在区间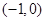 上是增函数,求实数
上是增函数,求实数 的取值范围;
的取值范围;
(3)当 时,若
时,若 ,在
,在 处取得最大值,求实数
处取得最大值,求实数 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2014届黑龙江省高二下学期期中考试理科数学试卷(解析版) 题型:解答题
已知定义在 上的函数
上的函数 ,其中
,其中 为常数.
为常数.
(1)若 是函数
是函数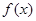 的一个极值点,求
的一个极值点,求 的值;
的值;
(2)若函数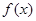 在区间
在区间 上是增函数,求
上是增函数,求 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com