
分析 (1)①求得a=|x-$\frac{1}{x}$|+x的分段函数式,作出函数y=|x-$\frac{1}{x}$|+x的图象,求出最值,即可得到所求a的范围;
②由①消去a,可得$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=2x2,求得1<x2≤2,即可得到所求范围;
(2)求得f(x)=$\left\{\begin{array}{l}{-{x}^{2}-ax,0≤x≤1}\\{{x}^{2}-ax-2,1<x≤2}\end{array}\right.$,对a讨论,当a≥4时,当2≤a<4时,当0≤a<2时,当-2<a<0时,当a≤-2时,讨论单调性,可得M(a),m(a),即可得到所求g(a)的解析式.
解答  解:(1)由f(x)+x2+1=0,x∈(0,2],
解:(1)由f(x)+x2+1=0,x∈(0,2],
得a=|x-$\frac{1}{x}$|+x=$\left\{\begin{array}{l}{\frac{1}{x},0<x≤1}\\{2x-\frac{1}{x},1<x≤2}\end{array}\right.$.
①作出函数y=$\left\{\begin{array}{l}{\frac{1}{x},0<x≤1}\\{2x-\frac{1}{x},1<x≤2}\end{array}\right.$图象,
由函数y的最小值为1,最大值为4-$\frac{1}{2}$=$\frac{7}{2}$.
在区间(0,2]上有两个不同的解,可得1<a≤$\frac{7}{2}$,
故a的取值范围是(1,$\frac{7}{2}$).
②∵x1<x2,a=$\frac{1}{{x}_{1}}$,a=2x2-$\frac{1}{{x}_{2}}$,
则有$\frac{1}{{x}_{1}}$=2x2-$\frac{1}{{x}_{2}}$,即$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=2x2,
又1<x2≤2,∴$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=2x2∈(2,4],
故$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$的取值范围是(2,4].
(2)f(x)=$\left\{\begin{array}{l}{-{x}^{2}-ax,0≤x≤1}\\{{x}^{2}-ax-2,1<x≤2}\end{array}\right.$,
当a≥4时,有-$\frac{a}{2}$<0,$\frac{a}{2}$≥2,f(x)在[0,2]上为减函数,
则g(a)=f(0)-f(2)=2a-2.
当2≤a<4时,有-$\frac{a}{2}$<0,1≤$\frac{a}{2}$<2,f(x)在[0,$\frac{a}{2}$]上为减函数,在[$\frac{a}{2}$,2]上为增函数,
此时m(a)=f($\frac{a}{2}$)=-2-$\frac{{a}^{2}}{4}$,M(a)=max{f(0),f(2)}=0,
则g(a)=$\frac{{a}^{2}}{4}$+2
当0≤a<2时,有-$\frac{a}{2}$<0,0≤$\frac{a}{2}$<1,f(x)在[0,1]上为减函数,在[1,2]上为增函数,
此时m(a)=f(1)=-1-a,M(a)=max{f(0),f(2)}=$\left\{\begin{array}{l}{2-2a,0≤a<1}\\{0,1≤a<2}\end{array}\right.$,
则g(a)=$\left\{\begin{array}{l}{3-a,0≤a<1}\\{a+1,1≤a<2}\end{array}\right.$.
当-2<a<0时,有0<-$\frac{a}{2}$<1,$\frac{a}{2}$<0,f(x)在[0,-$\frac{a}{2}$]上为增函数,在[-$\frac{a}{2}$,1]上为减函数,
在[1,2]上为增函数,
此时m(a)=min{f(0),f(1)}=$\left\{\begin{array}{l}{1-a,-1<a<0}\\{0,-2<a≤-1}\end{array}\right.$,
M(a)=max{f(-$\frac{a}{2}$),f(2)}=2-2a,
则g(a)=$\left\{\begin{array}{l}{3-a,-1<a<0}\\{2-2a,-2<a≤-1}\end{array}\right.$.
当a≤-2时,有$-\frac{a}{2}$≥1,$\frac{a}{2}$<0,f(x)在[0,2]上为增函数,
则g(a)=f(2)-f(0)=2-2a.
则g(a)=$\left\{\begin{array}{l}{2-2a,a≤-1}\\{3-a,-1≤a<1}\\{a+1,1≤a<2}\\{2+\frac{{a}^{2}}{4},2≤a<4}\\{2a-2,a≥4}\end{array}\right.$.
点评 本题考查分段函数的运用:求取值范围和最值,注意运用绝对值的意义和分类讨论和数形结合的思想方法,同时考查函数的单调性的运用,考查化简整理的运算能力,属于难题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 若l⊥m,m⊥n,则l∥n | B. | 若α⊥β,β⊥γ,则α∥γ | C. | 若α∥β,m⊥α,则m⊥β | D. | 若m∥α,m∥β,则α∥β |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
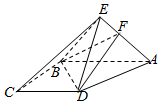 如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直,AB∥CD,AB⊥BC,AB=2CD=2BC=2,EA⊥EB,点F满足$\overrightarrow{AF}$=2$\overrightarrow{FE}$.
如图,直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直,AB∥CD,AB⊥BC,AB=2CD=2BC=2,EA⊥EB,点F满足$\overrightarrow{AF}$=2$\overrightarrow{FE}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在五面体ABCDEF中,四边形ABCD为菱形,且∠BAD=$\frac{π}{3}$,对角线AC与BD相交于O,OF⊥平面ABCD,BC=CE=DE=2EF=2.
如图,在五面体ABCDEF中,四边形ABCD为菱形,且∠BAD=$\frac{π}{3}$,对角线AC与BD相交于O,OF⊥平面ABCD,BC=CE=DE=2EF=2.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
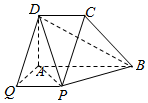 如图,在几何体ABCDQP中,AD⊥平面ABPQ,AB⊥AQ,AB∥CD∥PQ,CD=AD=AQ=PQ=$\frac{1}{2}$AB.
如图,在几何体ABCDQP中,AD⊥平面ABPQ,AB⊥AQ,AB∥CD∥PQ,CD=AD=AQ=PQ=$\frac{1}{2}$AB.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,+∞) | B. | (-∞,-2)∪(2,+∞) | C. | (-1,2) | D. | (-∞,-1)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com