
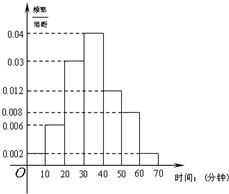
 某校高一年级共有学生320人.为调查高一年级学生每天晚自习自主支配学习时间(指除了完成教师布置的作业后学生根据自己的需要进行学习的时间)情况,学校采用随机抽样的方法从高一学生中抽取了n名学生进行问卷调查.根据问卷得到了这n名学生每天晚自习自主支配学习时间的数据(单位:分钟),按照以下区间分为七组:①[0,10),②[10,20),③[20,30),④[30,40),⑤[40,50),⑥[50,60),⑦[60,70),得到频率分布直方图如图.已知抽取的学生中每天晚自习自主支配学习时间低于20分钟的人数是4人.
某校高一年级共有学生320人.为调查高一年级学生每天晚自习自主支配学习时间(指除了完成教师布置的作业后学生根据自己的需要进行学习的时间)情况,学校采用随机抽样的方法从高一学生中抽取了n名学生进行问卷调查.根据问卷得到了这n名学生每天晚自习自主支配学习时间的数据(单位:分钟),按照以下区间分为七组:①[0,10),②[10,20),③[20,30),④[30,40),⑤[40,50),⑥[50,60),⑦[60,70),得到频率分布直方图如图.已知抽取的学生中每天晚自习自主支配学习时间低于20分钟的人数是4人.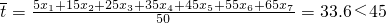
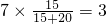 (人),第4组应抽
(人),第4组应抽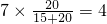 (人)
(人)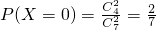 ,
,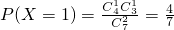 ,
,
| X | 0 | 1 | 2 |
| P |  |  |  |
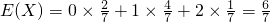
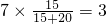 人,第4组应抽
人,第4组应抽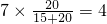 人.由题意知X=0,1,2,由此能求出X的分布列和期望.
人.由题意知X=0,1,2,由此能求出X的分布列和期望.

科目:高中数学 来源: 题型:
 某校高一年级共有学生320人.为调查高一年级学生每天晚自习自主支配学习时间(指除了完成教师布置的作业后学生根据自己的需要进行学习的时间)情况,学校采用随机抽样的方法从高一学生中抽取了n名学生进行问卷调查.根据问卷得到了这n名学生每天晚自习自主支配学习时间的数据(单位:分钟),按照以下区间分为七组:①[0,10),②[10,20),③[20,30),④[30,40),⑤[40,50),⑥[50,60),⑦[60,70),得到频率分布直方图如图.已知抽取的学生中每天晚自习自主支配学习时间低于20分钟的人数是4人.
某校高一年级共有学生320人.为调查高一年级学生每天晚自习自主支配学习时间(指除了完成教师布置的作业后学生根据自己的需要进行学习的时间)情况,学校采用随机抽样的方法从高一学生中抽取了n名学生进行问卷调查.根据问卷得到了这n名学生每天晚自习自主支配学习时间的数据(单位:分钟),按照以下区间分为七组:①[0,10),②[10,20),③[20,30),④[30,40),⑤[40,50),⑥[50,60),⑦[60,70),得到频率分布直方图如图.已知抽取的学生中每天晚自习自主支配学习时间低于20分钟的人数是4人.查看答案和解析>>
科目:高中数学 来源:山东省模拟题 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2011年山东省潍坊市高考模拟数学试卷(理科)(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2011年山东省潍坊市高考数学一模试卷(文科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com