练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    （09年济宁质检理）（14分）

    已知函数．

    （1）当时，求函数的单调区间和极值；

    （2）当时，若，均有，求实数的取值范围；

    （3）若，，且，试比较与的大小．

    解析：由题意，   ……………………………………………2分

    （1）当时，

    由得，解得，函数的单调增区间是；

    由得，解得，函数的单调增区间是

    ∴当时，函数有极小值为．………6分

    （2）当时，由于，均有，

    即，恒成立，

    ∴，，  ……………………………………………………8分

    由（1），函数极小值即为最小值，

    ∴，解得．………………………………10分

    （3），

    ∵且，

    ∴，

    ∴，……………………………………………12分

    又，∴，

    ∴，即．…………14分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    （09年济宁质检理）（12分）

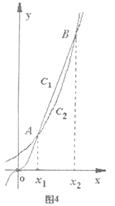
        函数和的图象的示意图如图4所示，设两函数的图象交于点，且

    （1）请指出示意图中分别对应哪一个函数？

    （2）若，且，指出a，b的值，并说明理由；

          （3）结合函数图象的示意图，判断的大小，并按从小到大的顺序排列。

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （09年济宁质检理）（12分）

    已知某类学习任务的掌握程度与学习时间（单位时间）之间的关系为

    ，这里我们称这一函数关系为“学习曲线”．已知这类学习任务中的某项任务有如下两组数据：．

    （1）试确定该项学习任务的“学习曲线”的关系式；

    （2）若定义在区间上的平均学习效率为，问这项学习任务从哪一刻开始的2个单位时间内平均学习效率最高．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （09年济宁质检理）（12分）

      已知函数．

    （1）求函数的最小正周期；

    （2）在给定的坐标系内，用五点作图法画出函数在一个周期内的图象．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （09年济宁质检理）（12分）

      数列的前项和记为，，．

    （1）当为何值时，数列是等比数列？

    （2）在（1）的条件下，若等差数列的前项和有最大值，且，又 成等比数列，求．

    查看答案和解析>>

    同步练习册答案