【答案】
分析:(1)整理a
n+12-a
na
n+1-2a
n2=0得(a
n+1-2a
n)(a
n+1+a
n)=0,进而求得a
n+1=2a
n,数列{a
n}是以2为首项,2为公比的等比数列,进而根据等比数列通项公式求得a
n,根据b
2=3,T
5=25.求得等差数列的首项和公差进而求得b
n.
(2)由(1)得T
n,进而求得
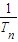
,先看当n=1时

<2,进而利用

<
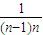
=
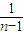
-
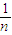
利用裂项法求和,进而求得
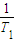
+
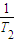
+…+
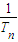
<2-
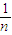
<2.
(3)令P
n=
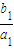
+
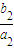
+…+
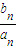
=

+
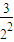
+
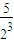
+…+
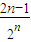
.把(1)中求得的a
n和b
n代入P
n,利用错位相减法求得P
n,进而判断P
n递增,求得P
n的范围,进而求得c的最小值.
解答:解:(1)a
n+12-a
na
n+1-2a
n2=0
得(a
n+1-2a
n)(a
n+1+a
n)=0,
由于数列{a
n}的每一项都是正数,∴a
n+1=2a
n,∴a
n=2
n.
设b
n=b
1+(n-1)d,由已知有b
1+d=3,5b
1+
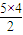
d=25,
解得b
1=1,d=2,∴b
n=2n-1.
(2)由(1)得T
n=n
2,∴
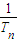
=
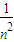
,
当n=1时,
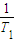
=1<2.
当n≥2时,
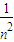
<
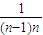
=
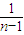
-
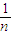
.
∴
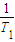
+
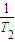
+…+
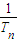
<1+

-

+

-

++
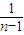
-
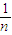
=2-
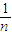
<2.
(3)记P
n=
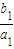
+
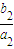
+…+
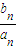
=

+
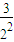
+
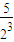
+…+
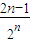
.
∴

P
n=
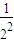
+
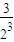
++
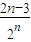
+
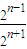
,
两式相减得P
n=3-
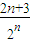
.
∵P
n递增,∴

≤P
n<3,P
4=
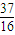
>2,
∴最小的整数c=3.
点评:本题主要考查了等差数列的性质和数列的求和问题.对于一些常用的数列的求和方法如公式法、错位相减法、叠加法、裂项法等应熟练掌握.

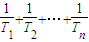 与2的大小;
与2的大小;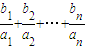 <c恒成立,求整数c的最小值.
<c恒成立,求整数c的最小值.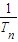 ,先看当n=1时
,先看当n=1时 <2,进而利用
<2,进而利用 <
<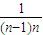 =
=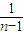 -
-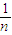 利用裂项法求和,进而求得
利用裂项法求和,进而求得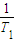 +
+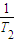 +…+
+…+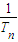 <2-
<2-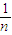 <2.
<2.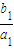 +
+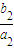 +…+
+…+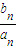 =
= +
+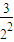 +
+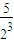 +…+
+…+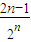 .把(1)中求得的an和bn代入Pn,利用错位相减法求得Pn,进而判断Pn递增,求得Pn的范围,进而求得c的最小值.
.把(1)中求得的an和bn代入Pn,利用错位相减法求得Pn,进而判断Pn递增,求得Pn的范围,进而求得c的最小值.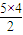 d=25,
d=25,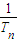 =
=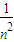 ,
,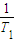 =1<2.
=1<2.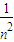 <
<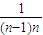 =
=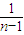 -
-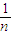 .
.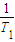 +
+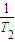 +…+
+…+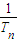 <1+
<1+ -
- +
+ -
- ++
++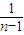 -
-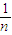 =2-
=2-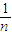 <2.
<2.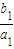 +
+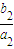 +…+
+…+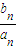 =
= +
+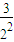 +
+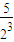 +…+
+…+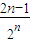 .
. Pn=
Pn=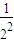 +
+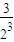 ++
++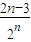 +
+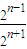 ,
,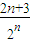 .
. ≤Pn<3,P4=
≤Pn<3,P4=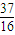 >2,
>2,

 名校课堂系列答案
名校课堂系列答案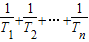 与2的大小;
与2的大小;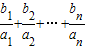 <c恒成立,求整数c的最小值.
<c恒成立,求整数c的最小值.