
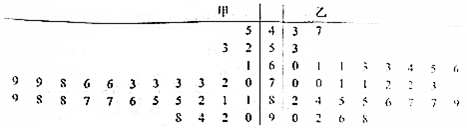
分析 (1)先求出甲校每位同学物理成绩被抽取的概率,由此能求出高二年级学生总数.
(2)由茎叶图可知甲校有22位同学分布在70至80之间,乙校有22位同学分布在60 至80之间,能由能得到统计结论.
(3)由茎叶图可知,甲校有3位同学成绩不及格,分别记为:a、b、c,乙校有3位同学成绩不及格,分别记为:A、B、C.由此利用列举法能求出至少抽到一名乙校学生的概率.
解答 解:(1)∵甲校每位同学物理成绩被抽取的概率均为0.15
∴高二年级学生总数$M=\frac{30}{0.15}=200$(2分)
(2)由茎叶图可知甲校有22位同学分布在70至80之间,
乙校有22位同学分布在60 至80之间,可得统计结论如下:
结论一:甲校的总体成绩分布下沉,所以平均数较大.
结论二:甲校的总体成绩更集中,方差较小.(4分)
所以,甲校学生的成绩较好.(6分)
(3)由茎叶图可知,甲校有3位同学成绩不及格,分别记为:a、b、c;
乙校有3位同学成绩不及格,分别记为:A、B、C.
则从两校不及格的同学中随机抽取两人有如下可能:
ab、ac、aA、aB、aC、bc、bA、bB、bC、cA、cB、cC、AB、AC、BC,
共有15个基本事件(8分)
其中,乙校至少有一名学生成绩不及格有如下可能:
aA、aB、aC、bA、bB、bC、cA、cB、cC、AB、AC、BC
共12个基本事件(10分)
∴$P=\frac{12}{15}=\frac{4}{5}$.(12分)
点评 本题考查茎叶图的应用,考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.


科目:高中数学 来源: 题型:解答题
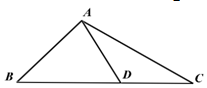 如图,在△ABC中,∠B=45°,D是BC边上一点,AB=$\frac{5}{2}\sqrt{6}$,AC=5$\sqrt{3}$,AD=5,∠ADB为锐角.
如图,在△ABC中,∠B=45°,D是BC边上一点,AB=$\frac{5}{2}\sqrt{6}$,AC=5$\sqrt{3}$,AD=5,∠ADB为锐角.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | 2 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{2}$+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (±3,0) | B. | (0,±3) | C. | (±9,0) | D. | (0,±9) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{4}$-y2=1 | B. | $\frac{{x}^{2}}{2}$-y2=1 | C. | $\frac{{x}^{2}}{3}$-$\frac{{y}^{2}}{3}$=1 | D. | x2-3y2=1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com