|
|
|
下列说法正确的是
|
| [ ] |
A. |
函数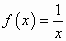 在其定义域上是减函数 在其定义域上是减函数
|
B. |
两个三角形全等是这两个三角形面积相等的必要条件
|
C. |
命题“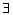 x∈R,x2+x+1>0”的否定是“ x∈R,x2+x+1>0”的否定是“ x∈R,x2+x+1<0” x∈R,x2+x+1<0”
|
D. |
给定命题p、q,若p∧q是真命题,则 p是假命题 p是假命题
|
|
|
练习册系列答案
相关习题
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
已知角α的顶点在原点,始边与x轴的正半轴重合,终边经过点P(-1,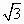 ). ).
(Ⅰ)求sin2α-tanα的值;
(Ⅱ)若函数f(x)=cos(x+α)cosα+sin(x+α)sinα,求函数g(x)=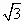 f( f( -2x)-2f2(x)+1在区间[0, -2x)-2f2(x)+1在区间[0, ]上的取值范围. ]上的取值范围.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
在区间(0,1)上任意取两个实数a,b,则a+b<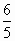 的概率为________. 的概率为________.
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
设函数y=f(x)在区间(a,b)的导函数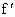 (x), (x),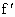 (x)在区间(a,b)的导函数 (x)在区间(a,b)的导函数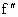 (x),若在区间(a,b)上的 (x),若在区间(a,b)上的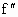 (x)<0恒成立,则称函数f(x)在区间(a,b)上为“凸函数”,已知 (x)<0恒成立,则称函数f(x)在区间(a,b)上为“凸函数”,已知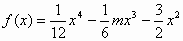 ,若当实数m满足|m|≤2时,函数f(x)在区间(a,b)上为“凸函数”,则b-a的最大值为 ,若当实数m满足|m|≤2时,函数f(x)在区间(a,b)上为“凸函数”,则b-a的最大值为
|
| [ ] |
A. |
1
|
B. |
2
|
C. |
3
|
D. |
4
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
某电视节目《幸运猜猜猜》有这样一个竞猜环节,一件价格为9816元的商品,选手只知道1,6,8,9四个数,却不知其顺序,若在竞猜中猜出正确价格中的两个或以上(但不含全对)正确位置,则正确位置会点亮红灯作为提示;若全对,则所有位置全亮白灯并选手赢得该商品,
(Ⅰ)求某选手在第一次竞猜时,亮红灯的概率;
(Ⅱ)若该选手只有二次机会,则他赢得这件商品的概率为多少?
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
若函数y=f(x)在R上可导,且满足不等x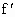 (x)>-f(x)恒成立,常数a,b满足a>b则下列不等式一定成立的是 (x)>-f(x)恒成立,常数a,b满足a>b则下列不等式一定成立的是
|
| [ ] |
A. |
af(b)>bf(a)
|
B. |
af(a)>bf(b)
|
C. |
af(a)<bf(b)
|
D. |
af(b)<bf(a)
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
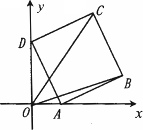
如图放置的正方形ABCD,AB=1,A,D分别在x轴、y轴的正半轴(含原点)上滑动,则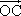 · ·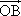 的最大值是________; 的最大值是________;
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
下表是最近十届奥运会的年份、届别、主办国,以及主办国在上届获得的金牌数、当届获得的金牌数的统计数据:
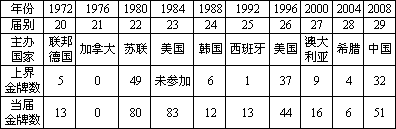
某体育爱好组织,利用上表研究所获金牌数与主办奥运会之间的关系,求出主办国在上届所获金牌数(设为x)与在当届所获金牌数(设为y)之间的线性回归方程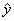 = =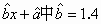 ,在2008年第29届北京奥运会上英国获得19块金牌,则据此线性回归方程估计在2012年第30届伦敦奥运会上英国将获得的金牌数为(所有金牌数精确到整数) ,在2008年第29届北京奥运会上英国获得19块金牌,则据此线性回归方程估计在2012年第30届伦敦奥运会上英国将获得的金牌数为(所有金牌数精确到整数)
|
| [ ] |
A. |
29块
|
B. |
30块
|
C. |
31块
|
D. |
32块
|
|
|
查看答案和解析>>
科目:高中数学
来源:课标综合版 专题复习
题型:
|
|
|
化简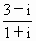 的结果为 的结果为
|
| [ ] |
A. |
1+2i
|
B. |
1–2i
|
C. |
2+i
|
D. |
2–i
|
|
|
查看答案和解析>>

 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案