
设奇函数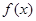 在
在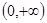 上是增函数,且
上是增函数,且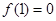 ,则不等式
,则不等式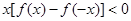 的解集为( )
的解集为( )
A. B.
B.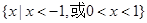
C.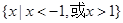 D.
D.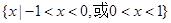
D
【解析】本试题主要是考查了抽象函数的单调性、奇偶性和不等式的求解问题。
∵函数f(x)是奇函数,函数f(x)在(0,+∞)上是增函数,
∴它在(-∞,0)上也是增函数.∵f(-x)=-f(x),
∴f(-1)=f(1)=0.不等式x[f(x)-f(-x)]<0可化为2xf(x)<0,
即xf(x)<0,∴当x<0时,可得f(x)>0=f(-1),∴x>-1,∴-1<x<0;当x>0时,可得f(x)<0=f(1),∴x<1,∴0<x<1.
综上,不等式x[f(x)-f(-x)]<0的解集为{x|-1<x<0,或0<x<1},故选D.
解决该试题的关键是将所求的不等式结合奇函数化简为xf(x)<0,然后分类讨论得到结论。


 口算题天天练系列答案
口算题天天练系列答案科目:高中数学 来源:2012-2013学年甘肃省高三9月第一次阶段性达标考试理科数学试卷(解析版) 题型:选择题
设奇函数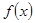 在
在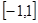 上是增函数,且
上是增函数,且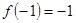 ,若
,若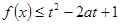 对所有的
对所有的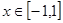 都成立,当
都成立,当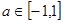 时,则
时,则 的取值范围是( )
的取值范围是( )
A.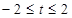 B.
B.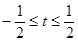
C.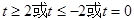 D.
D.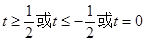
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖南省高三暑假自主学习检测理科数学试卷(解析版) 题型:选择题
设奇函数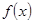 在
在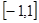 上是增函数,且
上是增函数,且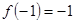 ,当
,当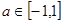 时,
时,
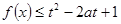 对所有的
对所有的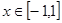 恒成立,则
恒成立,则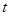 的取值范围是( )
的取值范围是( )
A.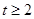 或
或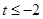 或
或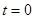 B.
B.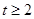 或
或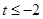
C.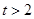 或
或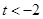 或
或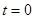 D.
D.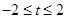
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江西省高三10月月考理科数学 题型:选择题
设奇函数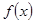 在
在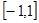 上是增函数,且
上是增函数,且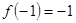 ,当
,当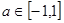 时,
时, 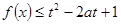 对所有的
对所有的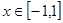 恒成立,则
恒成立,则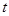 的取值范围是( )
的取值范围是( )
A.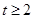 或
或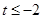 或
或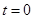 B.
B.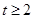 或
或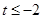
C.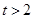 或
或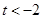 或
或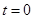 D.
D.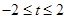
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com