

 ,
, =
= ,x∈(0,15),
,x∈(0,15), ,
, cm时,侧面积S最大,最大侧面积为
cm时,侧面积S最大,最大侧面积为 (cm2).
(cm2).  .
. =
= ,x∈(0,15),
,x∈(0,15),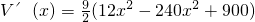 =0,得x=5,或x=15(舍去),
=0,得x=5,或x=15(舍去),| x | (0,5) | 5 | (5,15) |
| V'(x) | + | 0 | - |
| V(x) | ↗ | 极大值9 000 | ↘ |
 =
= .
. ,然后直接利用正六棱柱的侧面积公式写出侧面积,运用二次函数求最值;
,然后直接利用正六棱柱的侧面积公式写出侧面积,运用二次函数求最值;

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:

查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省苏州市张家港外国语学校高二(上)周日数学试卷10(理科)(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com