
在平面直角坐标系xOy中,过点A(-2,-1)椭圆C∶ =1(a>b>0)的左焦点为F,短轴端点为B1、B2,
=1(a>b>0)的左焦点为F,短轴端点为B1、B2, =2b2.
=2b2.
(1)求a、b的值;
(2)过点A的直线l与椭圆C的另一交点为Q,与y轴的交点为R.过原点O且平行于l的直线与椭圆的一个交点为P.若AQ·AR=3OP2,求直线l的方程.
(1)a=2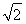 ,b=
,b=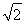 (2)当k=1时,直线l的方程为x-y+1=0,当k=-2时,直线l的方程为2x+y+5=0.
(2)当k=1时,直线l的方程为x-y+1=0,当k=-2时,直线l的方程为2x+y+5=0.
【解析】(1)因为F(-c,0),B1(0,-b),B2(0,b),所以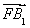 =(c,-b),
=(c,-b),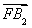 =(c,b).
=(c,b).
因为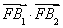 =2b2,
=2b2,
所以c2-b2=2b2.①
因为椭圆C过A(-2,-1),代入得,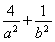 =1.②
=1.②
由①②解得a2=8,b2=2.
所以a=2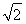 ,b=
,b=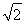 .
.
(2)由题意,设直线l的方程为y+1=k(x+2).
由 得(x+2)[(4k2+1)(x+2)-(8k+4)]=0.
得(x+2)[(4k2+1)(x+2)-(8k+4)]=0.
因为x+2≠0,所以x+2=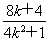 ,即xQ+2=
,即xQ+2=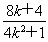 .
.
由题意,直线OP的方程为y=kx.
由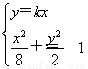 得(1+4k2)x2=8.则
得(1+4k2)x2=8.则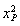 =
=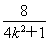 ,
,
因为AQ·AR=3OP2.所以|xQ-(-2)|×|0-(-2)|=3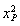 .
.
即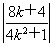 ×2=3×
×2=3×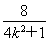 .
.
解得k=1,或k=-2.
当k=1时,直线l的方程为x-y+1=0,当k=-2时,直线l的方程为2x+y+5=0


科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用21练习卷(解析版) 题型:填空题
某校从高一年级学生中随机抽取部分学生,将他们的模块测试成绩分成6组:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知高一年级共有学生600名,据此估计,该模块测试成绩不少于60分的学生人数为________.

查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用16练习卷(解析版) 题型:解答题
如图,四棱柱ABCD-A1B1C1D1中,侧棱A1A⊥底面ABCD,AB∥DC,AB⊥AD,AD=CD=1,AA1=AB=2,E为棱AA1的中点.

(1)证明B1C1⊥CE;
(2)求二面角B1-CE-C1的正弦值;
(3)设点M在线段C1E上,且直线AM与平面ADD1A1所成角的正弦值为 ,求线段AM的长.
,求线段AM的长.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用13练习卷(解析版) 题型:填空题
如图,在平面直角坐标系xOy中,F1,F2分别为椭圆 =1(a>b>0)的左、右焦点,B,C分别为椭圆的上、下顶点,直线BF2与椭圆的另一个交点为D,若cos∠F1BF2=
=1(a>b>0)的左、右焦点,B,C分别为椭圆的上、下顶点,直线BF2与椭圆的另一个交点为D,若cos∠F1BF2= ,则直线CD的斜率为________.
,则直线CD的斜率为________.

查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用12练习卷(解析版) 题型:填空题
椭圆T: =1(a>b>0)的左、右焦点分别为F1,F2,焦距为2c.若直线y=
=1(a>b>0)的左、右焦点分别为F1,F2,焦距为2c.若直线y= (x+c)与椭圆T的一个交点M满足∠MF1F2=2∠MF2F1,则该椭圆的离心率等于________.
(x+c)与椭圆T的一个交点M满足∠MF1F2=2∠MF2F1,则该椭圆的离心率等于________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用11练习卷(解析版) 题型:解答题
已知以点C (t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(t∈R,t≠0)为圆心的圆与x轴交于点O,A,与y轴交于点O,B,其中O为原点.
(1)求证:△AOB的面积为定值;
(2)设直线2x+y-4=0与圆C交于点M,N,若|OM|=|ON|,求圆C的方程;
(3)在(2)的条件下,设P,Q分别是直线l:x+y+2=0和圆C上的动点,求|PB|+|PQ|的最小值及此时点P的坐标..
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮复习专题提升训练江苏专用10练习卷(解析版) 题型:填空题
在正项数列{an}中,a1=2,an+1=2an+3×5n,则数列{an}的通项公式为________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学(文)二轮专题复习与测试选择填空限时训练2练习卷(解析版) 题型:选择题
设a,b∈R,定义运算“∧”和“∨”如下:
a∧b= a∨b=
a∨b=
若正数a,b,c,d满足ab≥4,c+d≤4,则( )
A.a∧b≥2,c∧d≤2 B.a∧b≥2,c∨d≥2
C.a∨b≥2,c∧d≤2 D.a∨b≥2,c∨d≥2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com