
分析 化简可得1≤log2x≤3,y=(log2x-1)(log2x+2)=(log2x+$\frac{1}{2}$)2-$\frac{9}{4}$,从而求最值.
解答 解:∵一3≤log${\;}_{\frac{1}{2}}$x≤-1,
∴1≤log2x≤3,
y=log2$\frac{x}{2}$•log2(4x)
=(log2x-1)(log2x+2)
=(log2x+$\frac{1}{2}$)2-$\frac{9}{4}$,
故0≤(log2x+$\frac{1}{2}$)2-$\frac{9}{4}$≤10,
故当x=2时,函数有最小值0,
当x=8时,函数有最大值为10.
点评 本题考查了函数的最值的求法,本题应用了配方法,同时考查了整体思想的应用.


 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{5}$ | B. | -$\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | -$\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{-1+\sqrt{3}}{2}$ | B. | $\sqrt{3}$-$\sqrt{2}$ | C. | $\sqrt{2}$-1 | D. | $\frac{-1±\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
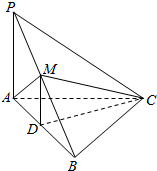 已知三棱锥P-ABC中,PA⊥平面ABC,底面ABC为边长等于3的正三角形,D、M为AB、PB中点,且△PAM为正三角形.
已知三棱锥P-ABC中,PA⊥平面ABC,底面ABC为边长等于3的正三角形,D、M为AB、PB中点,且△PAM为正三角形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com