C
分析:由已知的a比b长2,b比c长2判断得到a为最大边,根据大边对大角可得A为最大角,进而得到sinA的值为

,利用特殊角的三角函数值求出A的度数,可得cosA的值,然后用c表示出a和b,根据余弦定理表示出a
2,把表示出的a,b及cosA的值代入,可列出关于c的方程,求出方程的解即可得到c的值,从而确定出a与b的值,然后再由b,c及sinA的值,利用三角形的面积公式即可求出△ABC的面积.
解答:由题意a-b=2,且b-c=2,
得到a>b>c,可知A>B>C,即A为最大角,
所以sinA=

,所以A=60°或120°,
又A为最大角,所以A=120°,即cosA=-

,
由a-b=2,b-c=2变形得:a=c+4,b=c+2,
根据余弦定理a
2=b
2+c
2-2bc•cosA得:
(c+4)
2=(c+2)
2+c
2+c(c+2),
化简得:(c-3)(c+2)=0,
解得:c=3或c=-2(舍去),
所以a=7,b=5,又sinA=

,
则△ABC的面积S=

bcsinA=
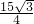
.
故选C
点评:此题考查了余弦定理,三角形的面积公式以及特殊角的三角函数值,根据三角形的边角关系得出A为最大角是本题的突破点,熟练掌握定理及公式,牢记特殊角的三角函数值是解本题的关键.同时要理解A不能为60°的理由:因为三个角互不相等,若A为60°,B和C都比60°小,则三个角之和小于180°,与三角形的内角和定理矛盾,故A不为60°,A应为120°.

 ,则△ABC的面积等于
,则△ABC的面积等于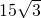

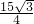
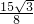
 ,利用特殊角的三角函数值求出A的度数,可得cosA的值,然后用c表示出a和b,根据余弦定理表示出a2,把表示出的a,b及cosA的值代入,可列出关于c的方程,求出方程的解即可得到c的值,从而确定出a与b的值,然后再由b,c及sinA的值,利用三角形的面积公式即可求出△ABC的面积.
,利用特殊角的三角函数值求出A的度数,可得cosA的值,然后用c表示出a和b,根据余弦定理表示出a2,把表示出的a,b及cosA的值代入,可列出关于c的方程,求出方程的解即可得到c的值,从而确定出a与b的值,然后再由b,c及sinA的值,利用三角形的面积公式即可求出△ABC的面积. ,所以A=60°或120°,
,所以A=60°或120°, ,
, ,
, bcsinA=
bcsinA=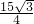 .
.
