
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,离心率为
,离心率为![]() ,点
,点![]() 为坐标原点,若椭圆
为坐标原点,若椭圆![]() 与曲线
与曲线![]() 的交点分别为
的交点分别为![]() (
(![]() 下
下![]() 上),且
上),且![]() 两点满足
两点满足![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)过椭圆![]() 上异于其顶点的任一点
上异于其顶点的任一点![]() ,作
,作![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() ,且直线
,且直线![]() 在
在![]() 轴、
轴、![]() 轴上的截距分别为
轴上的截距分别为![]() ,证明:
,证明:![]() 为定值.
为定值.
【答案】(1)![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)设![]() ,然后根据向量数量积求得
,然后根据向量数量积求得![]() 的值,再结合离心率求得
的值,再结合离心率求得![]() 的值,由此求得椭圆方程;(2).设点
的值,由此求得椭圆方程;(2).设点![]() ,然后根据条件求得
,然后根据条件求得![]() 的方程,从而求得直线
的方程,从而求得直线![]() 在
在![]() 轴、
轴、![]() 轴上的截距为
轴上的截距为![]() ,进而使问题得证.
,进而使问题得证.
试题解析:(1)设椭圆![]() 的半焦距为
的半焦距为![]() ,设
,设![]() ,则
,则![]() ,
,
由![]() ,得
,得![]() ,∴
,∴![]() ,①
,①
又椭圆![]() 的离心率为
的离心率为![]() ,所以
,所以![]() ,②
,②
又![]() ,③
,③
由①②③,解得![]() ,
,
故椭圆![]() 的标准方程为
的标准方程为![]() ................................... 6分
................................... 6分
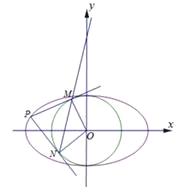
(2)如图,设点![]() ,由
,由![]() 是
是![]() 的切点知,
的切点知,![]() ,
,
所以![]() 四点在同一圆上,且圆的直径为
四点在同一圆上,且圆的直径为![]() ,
,
则圆心为![]() ,其方程为
,其方程为![]() ,
,
即![]() ,④
,④
即点![]() 满足话中④,又点
满足话中④,又点![]() 都在
都在![]() 上,
上,
所以![]() 坐标也满足方程
坐标也满足方程![]() ,⑤
,⑤
⑤-④得直线![]() 的方程为
的方程为![]() ,
,
令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() ,所以
,所以![]() ,
,
又点![]() 在椭圆
在椭圆![]() 上,所以
上,所以![]() ,即
,即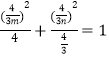 中,
中,
即![]() ,即
,即![]() 为定值.........................12分
为定值.........................12分


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:
【题目】首届世界低碳经济大会在南昌召开,本届大会以“节能减排,绿色生态”为主题,某单位在国家科研部门的支持下,进行技术攻关,采用了新式艺,把二氧化碳转化为一种可利用的化工产品,已知该单位每月的处理量最少为300吨,最多为600吨,月处理成本![]() (元)与月处理量
(元)与月处理量![]() (吨)之间的函数关系可近似地表示为
(吨)之间的函数关系可近似地表示为![]() ,且每处理一吨二氧化碳得到可利用的化工产品价值为200元.
,且每处理一吨二氧化碳得到可利用的化工产品价值为200元.
(1)该单位每月处理量为多少吨时,才能使每吨的平均处理成本最低?
(2)该单位每月能否获利?如果获利,求出最大利润;如果不获利,则需要国家至少补贴多少元才能使该单位不亏损?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知命题![]() 抛物线
抛物线![]() 的焦点
的焦点![]() 在椭圆
在椭圆![]() 上.命题
上.命题![]() 直线
直线![]() 经过抛物线
经过抛物线![]() 的焦点
的焦点![]() ,且直线
,且直线![]() 过椭圆
过椭圆![]() 的左焦点
的左焦点![]() ,
,![]() 是真命题.
是真命题.
(I)求直线![]() 的方程;
的方程;
(II)直线![]() 与抛物线相交于
与抛物线相交于![]() 、
、![]() ,直线
,直线![]() 、
、![]() ,分别切抛物线于
,分别切抛物线于![]() ,求
,求![]() 的交点
的交点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (其中
(其中![]() )
)
(Ⅰ) 若![]() 在其定义域内为单调递减函数,求
在其定义域内为单调递减函数,求![]() 的取值范围;
的取值范围;
(Ⅱ) 是否存在实数![]() ,使得当
,使得当![]() 时,不等式
时,不等式![]() 恒成立,如果存在,求
恒成立,如果存在,求![]() 的取值范围,如果不存在,说明理由(其中
的取值范围,如果不存在,说明理由(其中![]() 是自然对数的底数,
是自然对数的底数,![]() =2.71828…).
=2.71828…).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2009年推出一种新型家用轿车,购买时费用为![]() 万元,每年应交付保险费、养路费及汽油费共
万元,每年应交付保险费、养路费及汽油费共![]() 万元,汽车的维修费为:第一年无维修费用,第二年为
万元,汽车的维修费为:第一年无维修费用,第二年为![]() 万元,从第三年起,每年的维修费均比上一年增加
万元,从第三年起,每年的维修费均比上一年增加![]() 万元.
万元.
(1)设该辆轿车使用![]() 年的总费用(包括购买费用、保险费、养路费、汽油费及维修费)为
年的总费用(包括购买费用、保险费、养路费、汽油费及维修费)为![]() ,求
,求![]() 的表达式;
的表达式;
(2)这种汽车使用多少年报废最合算(即该车使用多少年,年平均费用最少)?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为实数).
为实数).
(1)当![]() 时,求函数
时,求函数![]() 的图象在点
的图象在点![]() 处的切线方程;
处的切线方程;
(2)设函数![]() (其中
(其中![]() 为常数),若函数
为常数),若函数![]() 在区间
在区间![]() 上不存在极值,且存在
上不存在极值,且存在![]() 满足
满足![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)已知![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com