已知指数函数f(x)=ax(a>0且a≠1).
(1)求f(x)的反函数g(x)的解析式;(2)解不等式:g(x)≤loga(2-3x).
解:(1)由y=a
x得x=log
ay且y>0,
即:y=log
ax,x>0,
所以函数y=a
x的反函数是g(x)=log
ax(a>0且a≠1)
(2)解:∵a>1,log
ax≤log
a(2-3x).
∴2-3x≥x>0
∴0<x

;
∵1>a>0,log
ax≤log
a(2-3x).
∴0<2-3x≤x
∴

≤x<

.
∴a>1原不等式的解集为
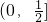
;0<a<1时,不等式的解集为
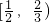
.
分析:(1)将y=a
x作为方程利用指数式和对数式的互化解出x,然后确定原函数的值域即得反函数的值域,问题得解.
(2)由a>1,g(x)≤log
a(2-3x),可得2-3x≥x>0,解不等式组可求;当1>a>0,log
ax≤log
a(2-3x).可得0<2-3x≤x,最后综合即可.
点评:本题属于基础性题,思路清晰、难度小,但解题中要特别注意指数式与对数式的互化,考查了利用对数函数的单调性解不等式,二次不等式的求解,解题中要注意,对对数的真数大于0的限制是解题中容易漏掉的考虑.

 ;
; ≤x<
≤x< .
.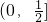 ;0<a<1时,不等式的解集为
;0<a<1时,不等式的解集为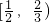 .
.

 阅读快车系列答案
阅读快车系列答案