练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】设函数.

    （1）讨论的单调性；

    （2）若对恒成立，求的取值范围.

    【答案】（1）当时，在上单调递增；当时，在上单调递增，在上单调递减；（2）.

    【解析】

    （1）分别在和两种情况下，根据的正负可确定的单调性；

    （2）根据（1）的结论可确定不合题意；当时，根据指数函数值域可知满足题意；当时，令，由此构造不等式求得结果.

    （1）由题意得：，

    当时，，在上单调递增；

    当时，令得：.

    当时，，在上单调递减；

    当时，，在上单调递增.

    综上所述：当时，在上单调递增；当时，在上单调递增，在上单调递减.

    （2）由（1）可知：当时，在上单调递增，

    当时，，，此时，不合题意；

    当时，恒成立，满足题意.

    当时，在处取最小值，且，

    令，解得：，此时恒成立.

    综上所述：的取值范围为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某医药研究所开发的一种新药，如果成年人按规定的剂量服用，据监测：服药后每毫升血液中的含药量y(微克)与时间t(小时)之间近似满足如图所示的曲线．

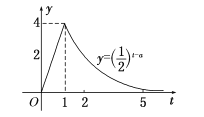
    (1)写出第一次服药后，y与t之间的函数关系式y＝f(t)；

    (2)据进一步测定：每毫升血液中含药量不少于0.25微克时，治疗有效．求服药一次后治疗有效的时间是多长？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】函数f(x)=Asin(wx+j)(A＞0，w＞0，-＜j＜，x∈R)的部分图象如图所示：，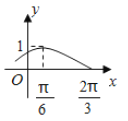

    (1)求函数y=f(x)的解析式；(2)当x∈时，求f(x)的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某高中为了了解高三学生每天自主参加体育锻炼的情况，随机抽取了100名学生进行调查，其中女生有55名.下面是根据调查结果绘制的学生自主参加体育锻炼时间的频率分布直方图：

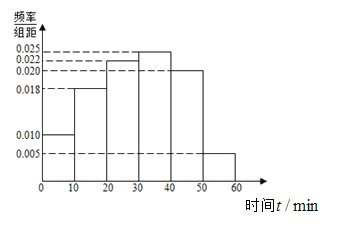
    将每天自主参加体育锻炼时间不低于40分钟的学生称为体育健康A类学生，已知体育健康A类学生中有10名女生.

    （Ⅰ）根据已知条件完成下面列联表，并据此资料你是否认为达到体育健康A类学生与性别有关？

    非体育健康A类学生

    体育健康A类学生

    合计

    男生

    女生

    合计

    （Ⅱ）将每天自主参加体育锻炼时间不低于50分钟的学生称为体育健康类学生，已知体育健康类学生中有2名女生，若从体育健康类学生中任意选取2人，求至少有1名女生的概率.

    附：

    P（）

    0.05

    0.010

    0.005

    3.841

    6.635

    7.879

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知圆C的圆心为(1，1)，直线与圆C相切.

    （1）求圆C的标准方程；

    （2）若直线过点(2，3)，且被圆C所截得的弦长为2，求直线的方程.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】同时具有性质：“① 最小正周期是；② 图象关于直线对称；③ 在上是单调递增函数”的一个函数可以是（ ）

    A.B.

    C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】ΔABC的内角A，B，C的对边分别为a，b，c，根据下列条件解三角形，其中有两解的是

    A. a=2，b=3，A=30°B. b=6，c=4，A=120°

    C. a=4，b=6，A=60°D. a=3，b=6，A=30°

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=sin（ωx-）（其中ω＞0）的图象上相邻两个最高点的距离为π．

    （Ⅰ）求函数f（x）的图象的对称轴；

    （Ⅱ）若函数y=f（x）-m在[0，π]内有两个零点x1，x2，求m的取值范围及cos（x1+x2）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某城市为了解游客人数的变化规律，提高旅游服务质量，收集并整理了2015年1月至2017年12月期间月接待游客量(单位：万人)的数据，绘制了下面的折线图．根据该折线图，下列结论错误的是（）

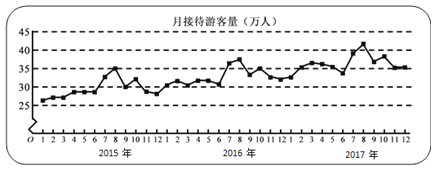
    A. 年接待游客量逐年增加

    B. 各年的月接待游客量高峰期在8月

    C. 2015年1月至12月月接待游客量的中位数为30万人

    D. 各年1月至6月的月接待游客量相对于7月至12月，波动性更小，变化比较平稳

    查看答案和解析>>

    同步练习册答案