
(1)AC=CE;
(2)AC2=DB2-BC2.

图
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:高中数学 来源: 题型:
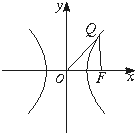 已知△OFQ的面积为2
已知△OFQ的面积为2| 6 |
| OF |
| FQ |
| 6 |
| 6 |
| OF |
| FQ |
| OF |
| ||
| 4 |
| OQ |
查看答案和解析>>
科目:高中数学 来源: 题型:
 已知△OFQ的面积为2
已知△OFQ的面积为2| 6 |
| OF |
| FQ |
| 6 |
| 6 |
| OF |
| FQ |
| OF |
| ||
| 4 |
| OQ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 6 |
| OF |
| FQ |
| 6 |
| 6 |
| OF |
| FQ |
| OF |
| ||
| 4 |
| OQ |

查看答案和解析>>
科目:高中数学 来源: 题型:
(12分)评委会把同学们上交的作品的件数按5天一组分组统计,绘制了频率分布直方 图,如图所示,已知从左到右各长方形的高的比为2:3:4:6:4:1,第三组的频数为 12 ,请解答下列问题:(1)本次活动共有多少件作品参加评比?
(2)那组上交的作品量最多?有多少件?
(3)经过评比,第四组和第六组分别有10件、2件作品获奖,问这两组哪组的获奖率高?
|

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com