
已知等差数列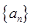 的前四项和为10,且
的前四项和为10,且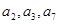 成等比数列
成等比数列
(1)求通项公式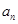
(2)设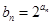 ,求数列
,求数列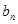 的前
的前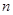 项和
项和 。
。
⑴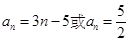 ;⑵
;⑵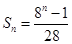 或
或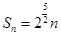 。
。
【解析】
试题分析:(1)利用等差数列的通项公式分别表示出前四项和与a2,a3,a7等比数列关系组成方程组求得a1和d,最后根据等差数列的通项公式求得an.
(2)把(1)中求得的an代入bn=2an中,可知数列{bn}为等比数列,进而根据等比数列的求和公式求得答案.
⑴由题意知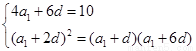
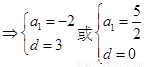
所以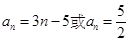 …………6分
…………6分
⑵当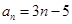 时,数列
时,数列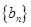 是首项为
是首项为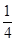 、公比为8的等比数列
、公比为8的等比数列
所以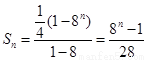 …………9分
…………9分
当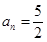 时,
时,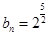 所以
所以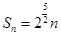
综上,所以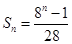 或
或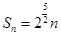 …………12分
…………12分
考点:本题主要考查了等差数列和等比数列的性质.考查了对数列通项公式和求和公式等基本知识的灵活运用.
点评:解决该试题的关键是利用等差数列的通项公式和等比数列的通项公式来求解通项公式,进而结合错位相减法得到求和。


 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案 小学学习好帮手系列答案
小学学习好帮手系列答案科目:高中数学 来源:2010-2011学年梅州市曾宪梓中学高一第二学期期末考试数学 题型:解答题
(本小题满分10分)
已知等差数列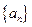 的前四项和为10,且
的前四项和为10,且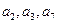 成等比数列。
成等比数列。
(1)求通项公式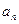 ; (2)设
; (2)设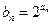 ,求数列
,求数列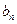 的前
的前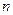 项和
项和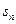
查看答案和解析>>
科目:高中数学 来源:2014届江苏连云港灌南高级中学高二上期中考试理数学试卷(解析版) 题型:解答题
(本小题满分14分)已知等差数列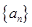 的前四项和为10,且
的前四项和为10,且 成等比数列
成等比数列
(1)求通项公式
(2)设 ,求数列
,求数列 的前
的前 项和
项和
查看答案和解析>>
科目:高中数学 来源:2011-2012学年山东省潍坊市高二寒假作业(四)数学试卷 题型:解答题
已知等差数列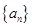 的前四项和为10,且
的前四项和为10,且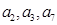 成等比数列
成等比数列
(1)求通项公式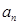 ,
,
(2)设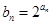 ,求数列
,求数列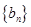 的前
的前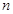 项和
项和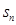 。
。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com