
已知等差数列![]() 的首项为a,公差为b,等比数列
的首项为a,公差为b,等比数列![]() 的首项为b,公比为a,其中a,b都是大于1的正整数,且
的首项为b,公比为a,其中a,b都是大于1的正整数,且![]() .
.
(1)求a的值;
(2)若对于任意的![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,求b的值;
成立,求b的值;
(3)令![]() ,问数列
,问数列![]() 中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.
中是否存在连续三项成等比数列?若存在,求出所有成等比数列的连续三项;若不存在,请说明理由.
(1)2(2)5(3)当![]() 时,不存在连续三项成等比数列;当
时,不存在连续三项成等比数列;当![]() 时,数列
时,数列![]() 中的第二、三、四项成等比数列,这三项依次是18,30,50.
中的第二、三、四项成等比数列,这三项依次是18,30,50.
(1)由已知,得![]() .由
.由![]() ,得
,得![]() .
.
因a,b都为大于1的正整数,故a≥2.又![]() ,故b≥3.再由
,故b≥3.再由![]() ,得
,得 ![]() .
.
由![]() ,故
,故![]() ,即
,即![]() .
.
由b≥3,故![]() ,解得
,解得![]() . 于是
. 于是![]() ,根据
,根据![]() ,可得
,可得![]() .
.
(2)由![]() ,对于任意的
,对于任意的![]() ,均存在
,均存在![]() ,使得
,使得![]() ,则
,则
![]() .
.
又![]() ,由数的整除性,得b是5的约数.
,由数的整除性,得b是5的约数.
故![]() ,b=5.
,b=5.
所以b=5时,存在正自然数![]() 满足题意.
满足题意.
(3)设数列![]() 中,
中,![]() 成等比数列,由
成等比数列,由![]() ,
,![]() ,得
,得
![]() .
.
化简,得![]() . (※)
. (※)
当![]() 时,
时,![]() 时,等式(※)成立,而
时,等式(※)成立,而![]() ,不成立.
,不成立.
当![]() 时,
时,![]() 时,等式(※)成立.当
时,等式(※)成立.当![]() 时,
时,![]() ,这与b≥3矛盾.
,这与b≥3矛盾.
这时等式(※)不成立.
综上所述,当![]() 时,不存在连续三项成等比数列;当
时,不存在连续三项成等比数列;当![]() 时,数列
时,数列![]() 中的第二、三、四项成等比数列,这三项依次是18,30,50.
中的第二、三、四项成等比数列,这三项依次是18,30,50.


科目:高中数学 来源: 题型:
(08年潍坊市二模)(14分)已知等差数列![]() 的首项为a,公差为b;等比数列
的首项为a,公差为b;等比数列![]() 的首项为b,公比为a,其中a,
的首项为b,公比为a,其中a,![]() ,且
,且![]() .
.
(1)求a的值;
(2)若对于任意![]() ,总存在
,总存在![]() ,使
,使![]() ,求b的值;
,求b的值;
(3)在(2)中,记![]() 是所有
是所有![]() 中满足
中满足![]() ,
, ![]() 的项从小到大依次组成的数列,又记
的项从小到大依次组成的数列,又记![]() 为
为![]() 的前n项和,
的前n项和,![]()
![]() 的前n项和,求证:
的前n项和,求证:![]() ≥
≥![]()
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知等差数列![]() 的首项为a,公差为b;等比数列
的首项为a,公差为b;等比数列![]() 的首项为b,公比为a,其中a,
的首项为b,公比为a,其中a,![]() ,且
,且![]() .
.
(1)求a的值;
(2)若对于任意![]() ,总存在
,总存在![]() ,使
,使![]() ,求b的值;
,求b的值;
(3)在(2)中,记![]() 是所有
是所有![]() 中满足
中满足![]() ,
, ![]() 的项从小到大依次组成的数列,又记
的项从小到大依次组成的数列,又记![]() 为
为![]() 的前n项和,
的前n项和,![]()
![]() 的前n项和,求证:
的前n项和,求证:![]() ≥
≥![]()
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江西南昌10所省高三第二次模拟突破冲刺文科数学(二)(解析版) 题型:填空题
已知等差数列 的首项为
的首项为 ,公差为
,公差为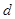 ,其前
,其前 项和为
项和为 ,若直线
,若直线 与圆
与圆 的两个交点关于直线
的两个交点关于直线 对称,则
对称,则 =
=
查看答案和解析>>
科目:高中数学 来源:2014届江西省高一下学期第二次月考数学试卷(解析版) 题型:解答题
已知等差数列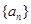 的首项为a,公差为b,等比数列
的首项为a,公差为b,等比数列 的首项为b,公比为a,其中a,b均为正整数,若
的首项为b,公比为a,其中a,b均为正整数,若 。
。
(1)求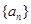 、
、 的通项公式;
的通项公式;
(2)若 成等比数列,求数列
成等比数列,求数列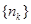 的通项公式。
的通项公式。
(3)设
 的前n项和为
的前n项和为 ,求当
,求当 最大时,n的值。
最大时,n的值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com