如图，正三角形ABC与直角三角形BCD成直二面角，且∠BCD=90°，∠CBD=30°.
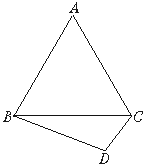
(1)求证：AB⊥CD；
(2)求二面角D—AB—C的大小；
(3)求异面直线AC和BD所成的角.
答案：(1)证明：∵平面ABC⊥平面BCD，且∠BCD=90°， ∴CD⊥平面ABC，∵AB ∴CD⊥AB. (2)解：过点C作CM⊥AB于M，连DM，由(1)知CD⊥平面ABC， ∴DM⊥AB. ∴∠CMD是二面角D—AB—C的平面角. 设CD=1，由∠BCD=90°，∠CBD=30°，得 ∵△ABC为正三角形，∴ ∴二面角D—AB—C的大小为 (3)解：取三边AB，AD，BC的中点M，N，O，连AO，MO，NO，MN，OD. 则OM ∴直线OM与MN所成的锐角或直角就是直线AC和BD所成的角. ∵△ABC为正三角形，且平面ABC⊥平面BCD， ∴AO⊥平面BCD，∴△AOD是直角三角形， 又∵CD⊥平面ABC，∴ 在△OMN中， 
练习册系列答案
相关习题
科目：高中数学 来源： 题型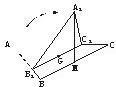：  如图，正三角形ABC的边长为3，过其中心G作BC边的平行线，分别交AB、AC于B1、C1．将△AB1C1沿B1C1折起到△A1B1C1的位置，使点A1在平面BB1C1C上的射影恰是线段BC的中点M．求：（1）二面角A1-B1C1-M的大小； （2）异面直线A1B1与CC1所成角的大小．（用反三角函数表示） 查看答案和解析>> 科目：高中数学 来源： 题型： 如图①，正三角形ABC边长2，CD为AB边上的高，E、F分别为AC、BC中点，现将△ABC沿CD翻折成直二面角A-DC-B，如图② （1）判断翻折后直线AB与面DEF的位置关系，并说明理由 （2）求二面角B-AC-D的余弦值 （3）求点C到面DEF的距离 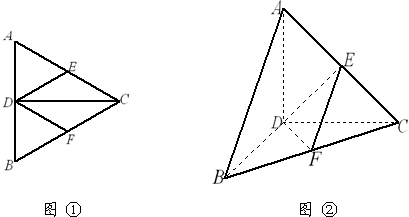 查看答案和解析>> 科目：高中数学 来源： 题型： 如图,在正三角形ABC中,D、E、F分别为各边的中点,G、H、I、J分别为AF、AD、BE、DE的中点,将△ABC沿DE、EF、DF折成三棱锥以后,GH与IJ所成角的度数为_____________.
查看答案和解析>> 科目：高中数学 来源：2012年人教A版高中数学必修二空间点、直线、平面之间的位置关系练习卷（二） 题型：解答题 如图，正三角形ABC的边长为2，D、E、F分别为各边的中点将△ABC沿DE、EF、DF折叠，使A、B、C三点重合，构成三棱锥A— DEF ．
(I)求平面ADE与底面DEF所成二面角的余弦值 (Ⅱ)设点M、N分别在AD、EF上， ①当λ为何值时，MN为异面直线AD与EF的公垂线段? 请证明你的结论②设异面直线MN与AE所成的角为a，异面直线MN与DF所成的角为β，试求a+β 的值
查看答案和解析>> 同步练习册答案 湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com版权声明：本站所有文章，图片来源于网络，著作权及版权归原作者所有，转载无意侵犯版权，如有侵权，请作者速来函告知，我们将尽快处理，联系qq：3310059649。 ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号 |
平面ABC，
，BD=2.
，
.∴
，∴∠
.
.
，MN
.
，
，MN=1，ON=1，
(λ＞O，λ为变量)