
(08年沈阳二中四模理)(14分)已知点![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在直线
在直线![]() 上,且满足
上,且满足![]() ,
,![]()
![]() 。
。
(Ⅰ)当点![]() 在
在![]() 轴上移动时,求点
轴上移动时,求点![]() 的轨迹
的轨迹![]() ;
;
(Ⅱ)过定点![]() 作直线
作直线![]() 交轨迹
交轨迹![]() 于
于![]() 两点,
两点,![]() 是
是![]() 点关于坐标原点
点关于坐标原点![]() 的对称点,求证:
的对称点,求证:![]() ;
;
(Ⅲ)在(Ⅱ)中,是否存在垂直于![]() 轴的直线
轴的直线![]() 被以
被以![]() 为直径的圆截得的弦长恒为定值?若存在求出
为直径的圆截得的弦长恒为定值?若存在求出![]() 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。
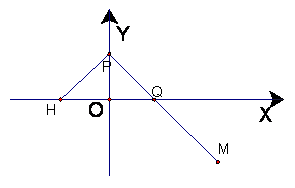
解析:(Ⅰ)设![]()
![]()
![]()
![]() 且
且![]()
![]()
![]() ………………………………4分
………………………………4分
∴动点M的轨迹C是以O(0,0)为顶点,以(1,0)为焦点的抛物线(除去原点)…5分
(Ⅱ)解:依题意,设直线![]() 的方程为
的方程为![]() ,
,
![]() ,则A,B两点的坐标满足
,则A,B两点的坐标满足
方程组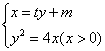 消去
消去![]() 并整理得:
并整理得:![]()
![]() …………………………………7分
…………………………………7分
设直线AE和BE的斜率分别为![]() ,则
,则
![]() =
=![]()
![]()
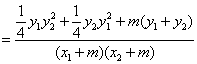
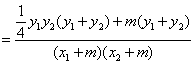
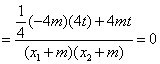 …………………………9分
…………………………9分
![]()
![]()
![]() ,
,![]()
![]() .…………………………10分
.…………………………10分
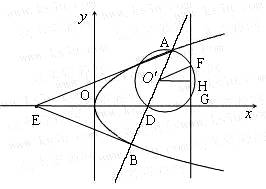
(Ⅲ)假设存在满足条件的直线![]() ,其方程为
,其方程为![]() ,AD的中点为
,AD的中点为![]() ,
,![]() 与AD为直径的圆相交于点F、G,FG的中点为H,则
与AD为直径的圆相交于点F、G,FG的中点为H,则![]() ,
,![]() 点的坐标为
点的坐标为![]() .
.
![]()
![]()
![]()
![]()
![]()
![]() ……………………………12分
……………………………12分
![]()
令![]() ,得
,得![]() ,此时,
,此时,![]()
∴当![]() ,即
,即![]() 时,
时,![]() (定值)
(定值)
∴当![]() 时,满足条件的直线
时,满足条件的直线![]() 存在,其方程为
存在,其方程为![]() ;当
;当![]() 时,满足条件的直线
时,满足条件的直线![]() 不存在. ………………………………………14分
不存在. ………………………………………14分


科目:高中数学 来源: 题型:
(08年沈阳二中四模理)(12分) 在一次智力测试中,有两个相互独立的题目![]() 、
、![]() ,答题规则为:被测试者答对问题
,答题规则为:被测试者答对问题![]() 可得分数为
可得分数为![]() ,答对问题
,答对问题![]() 的分数为
的分数为![]() ,没有答对不得分。先答哪个题目由被测试者自由选择,但只有第一个问题答对,才能再答第二题,否则终止答题。若你是被测试者,且假设你答对问题
,没有答对不得分。先答哪个题目由被测试者自由选择,但只有第一个问题答对,才能再答第二题,否则终止答题。若你是被测试者,且假设你答对问题![]() 、
、![]() 的概率分别为
的概率分别为![]()
(1)若![]() ,你应如何依据题目分值选择先答哪一题目?
,你应如何依据题目分值选择先答哪一题目?
(2)若已知![]() ,当
,当![]() 满足怎样的关系时,你选择先答题
满足怎样的关系时,你选择先答题![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年沈阳二中四模文) 某小组有男生、女生若干人,如果从中选一人参加某项测试,女生被选中的概率是![]() ;如果从中选两人参加测试,两人都是女生的概率为
;如果从中选两人参加测试,两人都是女生的概率为![]() (每个人被选中是等可能的)。
(每个人被选中是等可能的)。
(Ⅰ)求该小组男生、女生各多少人?
(Ⅱ)从该小组选出3人,求男女生都有的概率;
(Ⅲ)若对该小组的同学进行某项测试,其中女生通过的概率为![]() ,男生通过的概率为
,男生通过的概率为![]() ,现对该小组中男生甲、乙和女生丙三人进行测试,求至少有两人通过测试的概率
,现对该小组中男生甲、乙和女生丙三人进行测试,求至少有两人通过测试的概率
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年沈阳二中四模)(12分)已知数列![]() 有
有![]() ,
,![]() (常数
(常数 ![]() ),对任意的正整数
),对任意的正整数![]() ,
,![]() ,并有
,并有![]() 满足
满足![]() 。
。
(1)求![]() 的值;
的值;
(2)试确定数列![]() 是否是等差数列,若是,求出其通项公式,若不是,说明理由;
是否是等差数列,若是,求出其通项公式,若不是,说明理由;
(3)(理科生答文科生不答)对于数列![]() ,假如存在一个常数
,假如存在一个常数![]() 使得对任意的正整数
使得对任意的正整数![]() 都有
都有![]() ,且
,且![]() ,则称
,则称![]() 为数列
为数列![]() 的“上渐近值”,令
的“上渐近值”,令![]() ,求数列
,求数列![]() 的“上渐近值”。
的“上渐近值”。
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年沈阳二中四模理)(14分)已知点![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在直线
在直线![]() 上,且满足
上,且满足![]() ,
,![]()
![]() 。
。
(Ⅰ)当点![]() 在
在![]() 轴上移动时,求点
轴上移动时,求点![]() 的轨迹
的轨迹![]() ;
;
(Ⅱ)过定点![]() 作直线
作直线![]() 交轨迹
交轨迹![]() 于
于![]() 两点,
两点,![]() 是
是![]() 点关于坐标原点
点关于坐标原点![]() 的对称点,求证:
的对称点,求证:![]() ;
;
(Ⅲ)在(Ⅱ)中,是否存在垂直于![]() 轴的直线
轴的直线![]() 被以
被以![]() 为直径的圆截得的弦长恒为定值?若存在求出
为直径的圆截得的弦长恒为定值?若存在求出![]() 的方程;若不存在,请说明理由。
的方程;若不存在,请说明理由。

查看答案和解析>>
科目:高中数学 来源: 题型:
(08年沈阳二中四模文) 已知点![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴的正半轴上,点
轴的正半轴上,点![]() 在直线
在直线![]() 上,且满足
上,且满足![]() ,
,![]()
![]() 。
。
(Ⅰ)当点![]() 在
在![]() 轴上移动时,求点
轴上移动时,求点![]() 的轨迹
的轨迹![]() ;
;
(Ⅱ)过定点![]() 作直线
作直线![]() 交轨迹
交轨迹![]() 于
于![]() 两点,试问在
两点,试问在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 成立;
成立;

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com