
(本题满分14分)二次函数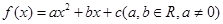 满足条件:
满足条件:
①当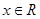 时,
时,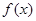 的图象关于直线
的图象关于直线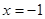 对称;
对称;
② 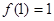 ;
;
③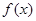 在
在 上的最小值为
上的最小值为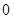 ;
;
(1)求函数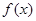 的解析式;
的解析式;
(2)求最大的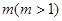 ,使得存在
,使得存在 ,只要
,只要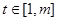 ,就有
,就有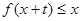 .
.
解:(1)∵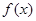 的对称轴为
的对称轴为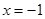 ,
,
∴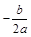 = –1即
= –1即 ………………1分
………………1分
又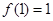 ,即
,即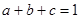 …………………………2分
…………………………2分
由条件③知: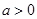 ,且
,且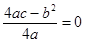 ,即
,即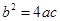 ……………………3分
……………………3分
由上可求得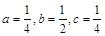 ……………………4分
……………………4分
∴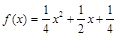 …………………………5分.
…………………………5分.
(2)由(1)知: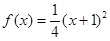 ,图象开口向上.
,图象开口向上.
而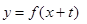 的图象是由
的图象是由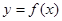 平移
平移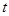 个单位得到,要
个单位得到,要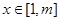 时,
时, 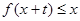 即
即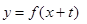 的图象在
的图象在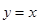 的图象的下方,且
的图象的下方,且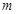 最大.……7分
最大.……7分
∴1,m应该是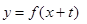 与
与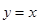 的交点横坐标,……………………8分
的交点横坐标,……………………8分
即1,m是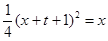 的两根,…………………………9分
的两根,…………………………9分
由1是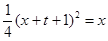 的一个根,得
的一个根,得 ,解得
,解得 ,或
,或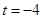 …11分
…11分
把 代入原方程得
代入原方程得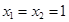 (这与
(这与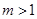 矛盾)………………12分
矛盾)………………12分
把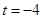 代入原方程得
代入原方程得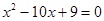 ,解得
,解得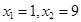 ∴
∴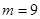 ……13分
……13分
综上知: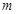 的最大值为9.……………………14分
的最大值为9.……………………14分
【解析】略


 名师点拨卷系列答案
名师点拨卷系列答案科目:高中数学 来源: 题型:
(本题满分14分)本题共有2个小题,第1小题满分7分,第2小题满分7分.
已知二次函数![]()
![]() 对任意
对任意![]() 均有
均有![]() 成立,且函数的图像过点
成立,且函数的图像过点![]()
![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)若不等式![]() 的解集为
的解集为![]() ,求实数
,求实数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源:2014届广东省高二上学期期末考试文科数学试卷(解析版) 题型:解答题
(本题满分14分)
已知二次函数 +
+ 的图象通过原点,对称轴为
的图象通过原点,对称轴为 ,
, .
. 是
是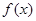 的导函数,且
的导函数,且
 .
.
(1)求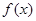 的表达式(含有字母
的表达式(含有字母 );
);
(2)若数列 满足
满足 ,且
,且 ,求数列
,求数列 的通项公式;
的通项公式;
(3)在(2)条件下,若 ,
, ,是否存在自然数
,是否存在自然数 ,使得当
,使得当 时
时
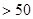 恒成立?若存在,求出最小的
恒成立?若存在,求出最小的 ;若不存在,说明理由.
;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年浙江省六校高三4月月考考试数学理卷 题型:解答题
(本题满分14分)
如图一,平面四边形ABCD关于直线AC对称,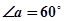 ,
,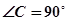 ,
,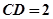 。
。
把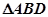 沿BD折起(如图二),使二面角A-BD-C的余弦值等于
沿BD折起(如图二),使二面角A-BD-C的余弦值等于 。对于图二,
。对于图二,
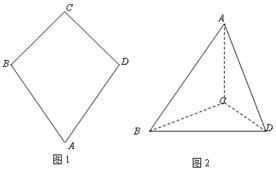
(1)求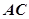 的长,并证明:
的长,并证明: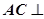 平面
平面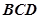 ;
;
(2)求直线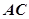 与平面
与平面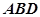 所成角的正弦值。
所成角的正弦值。
查看答案和解析>>
科目:高中数学 来源:2010-2011学年方城一高高三年级10月月考数学试卷(理科) 题型:解答题
(本题满分14分)已知二次函数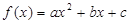 .
.
(1)若a>b>c, 且f(1)=0,证明f(x)的图象与x轴有2个交点;
(2)若 对 ,方程
,方程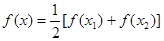 有2个不等实根,
有2个不等实根,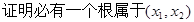 ;
;
(3)在(1)的条件下,是否存在m∈R,使f(m)=- a成立时,f(m+3)为正数,若
存在,证明你的结论,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com