解:(1)由定义在R上奇函数f(x)=ax
3+bx
2+cx+d(a≠0),可得 b=d=0,故f(x)=ax
3 +cx.
再由f(1)≠1可得a+c≠1.
当x∈[1,2]时,函数

=ax
2+c,当a>0时,g(x)在[1,2]上是增函数,再根据它的值域为[-2,1],
可得 a+c=-2,4a+c=1,解得 a=1,c=-3,故f(x)=x
3 -3.
当a<0时,g(x)=ax
2+c 在[1,2]上是减函数,可得a+c=1,不满足a+c≠1,故舍去.
综上可得,f(x)=x
3 -3.
(2)根据函数f(x)=x
3 -3,可得在[1,+∞)是增函数.
令它的导数为f′(x)=3x
2>0,可得x>0,或 x<0,故函数的增区间为(-∞,0)、(0,+∞),即此函数的增区间为(-∞,+∞),此函数无减区间.
(3)关于x的方程f(x)-t=0的根的个数,即函数y=f(x)与函数y=t 的交点的个数.
结合图象可得,函数y=f(x)与函数y=t 的交点的个数为1.
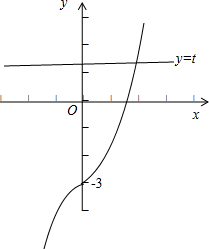
分析:(1)由定义在R上奇函数f(x)=ax
3+bx
2+cx+d(a≠0),可得 b=d=0,函数 g(x)=ax
2+c,当a>0时,g(x)在[1,2]上是增函数,再根据它的值域为[-2,1],
可得 a+c=-2,4a+c=1,解得 a=1,c=-3,从而得到f(x)的解析式.当a<0时,g(x)=ax
2+c 在[1,2]上是减函数,可得a+c=1,不满足f(1)≠1,故舍去.
(2)根据函数f(x)=x
3 -3,可得在[1,+∞)是增函数.令它的导数为f′(x)=3x
2>0,可得x的范围,即可得到增区间,此函数无减区间.
(3)关于x的方程f(x)-t=0的根的个数,即函数y=f(x)与函数y=t 的交点的个数.结合图象,可得结论.
点评:本题主要考查方程的根的存在性及个数判断,求函数的解析式和单调区间,函数的奇偶性的应用,体现了化归与转化、分类讨论的数学思想,属于中档题.

 的值域为[-2,1].
的值域为[-2,1]. =ax2+c,当a>0时,g(x)在[1,2]上是增函数,再根据它的值域为[-2,1],
=ax2+c,当a>0时,g(x)在[1,2]上是增函数,再根据它的值域为[-2,1],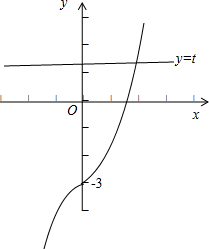


 通城学典默写能手系列答案
通城学典默写能手系列答案 已知定义在R上奇函数f(x)在x≥0时的图象如图所示,
已知定义在R上奇函数f(x)在x≥0时的图象如图所示,