
(2007
天津,19)如下图,在四棱锥P—ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,E是PC的中点.(1)
证明CD⊥AE;(2)
证明PD⊥平面ABE;(3)
求二面角A-PD-C的大小.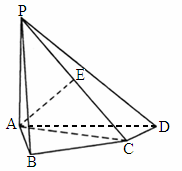
|
解析: (1)在四棱锥P-ABCD中,因PA⊥底面ABCD,CD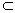 平面ABCD,故PA⊥CD. 平面ABCD,故PA⊥CD.
∵ AC⊥CD,PA∩AC=A,∴CD⊥平面PAC.而AE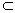 平面PAC,∴CD⊥AE. 平面PAC,∴CD⊥AE.
(2) 由PA=AB=BC,∠ABC=60°,可得AC=PA.∵E是PC的中点,∴AE⊥PC.由 (1)知,AE⊥CD,且PC∩CD=C,所以AE⊥平面PCD.而 PD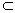 平面PCD,∴AE⊥PD. 平面PCD,∴AE⊥PD.
∵ PA⊥底面ABCD,PD在底面ABCD内的射影是AD,AB⊥AD,∴AB⊥PD.又∵ AB∩AE=A,综上得PD⊥平面ABE.(3) 过点A作AM⊥PD,垂足为M,连结EM.由(2)知,AE⊥平面PCD,AM在平面PCD内的射影是EM,则EM⊥PD.
因此∠ AME是二面角A-PD-C的平面角.由已知,得∠ CAD=30°,设AC=a,可得PA=a,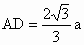 . .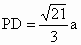 , , . .
在 Rt△ADP中,∵AM⊥PD,∴ 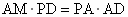 ,则 ,则
在 Rt△AEM中,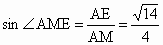 . .
所以二面角 A-PD-C的大小是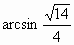 . . |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com