
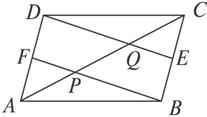
图1-1-14
思路分析:在△ADQ中,F是AD的中点,只要证明FP∥DQ,即可由推论1得AP=PQ;同理在△CPB中,根据E是BC的中点,EQ∥BP,由推论1得CQ=PQ,由此得到结论.
证明:∵四边形ABCD是平行四边形,E、F分别是BC、AD边上的中点,
∴四边形BEDF是平行四边形(一组对边平行且相等的四边形一定是平行四边形).
∵在△ADQ中,F是AD的中点,FP∥DQ,
∴P是AQ的中点.∴AP=PQ.
在△CPB中,E是BC的中点,EQ∥BP.
∴Q是CP的中点.∴CQ=PQ.
∴AP=PQ=QC.
深化升华 本题两次利用了E、F是中点的条件,在利用平行线等分线段定理或推论时要把平行和中点两个条件摆齐.


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源:2012-2013学年湖北省荆门市高三元月调考文科数学试卷(解析版) 题型:填空题
在平行四边形ABCD中,E和F分别是边CD和BC的中点,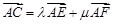 ,其中
,其中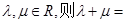 ___________.
___________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com