
【题目】某工厂为提高生产效率,开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名工人,将他们随机分成两组,每组20人.第一组工人用第一种生产方式,第二组工人用第二种生产方式.根据工人完成生产任务的工作时间(单位:min)绘制了如下茎叶图:
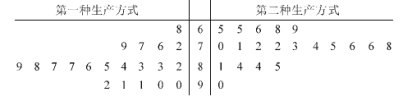
(1)求40名工人完成生产任务所需时间的中位数m,并将完成生产任务所需时间超过m和不超过m的工人数填入下面的列联表:
超过m | 不超过m | 总计 | |
第一种生产方式 | |||
第二种生产方式 | |||
总计 |
(2)根据(1)中的列联表,能否有![]() 的把握认为两种生产方式的效率有差异?
的把握认为两种生产方式的效率有差异?
附: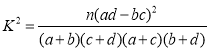
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
科目:高中数学 来源: 题型:
【题目】若![]() 、
、![]() 、
、![]() 均为正整数,且
均为正整数,且![]() ,
,![]() 为一素数,
为一素数,![]() 、
、![]() 、
、![]() 的
的![]() 进制表示分别为
进制表示分别为![]() ,其中,
,其中,![]() .证明:
.证明:
(1)若![]() ,且对整数
,且对整数![]()
![]() 均有
均有![]() ,则
,则![]() ,其中,
,其中,![]() 表示不超过实数
表示不超过实数![]() 的最大整数.
的最大整数.
(2)![]()
![]() ,其中,
,其中,![]() 表示集合A中元素的个数.
表示集合A中元素的个数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,
,![]() .
.
(Ⅰ)若![]() 为偶函数,求
为偶函数,求![]() 的值并写出
的值并写出![]() 的增区间;
的增区间;
(Ⅱ)若关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,当
,当![]() 时,求
时,求![]() 的最小值;
的最小值;
(Ⅲ)对任意的![]() ,
,![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
如图,已知椭圆![]() 的离心率为
的离心率为![]() ,以该椭圆上的点和椭圆的左、右焦点
,以该椭圆上的点和椭圆的左、右焦点![]() 为顶点的三角形的周长为
为顶点的三角形的周长为![]() .一等轴双曲线的顶点是该椭圆的焦点,设
.一等轴双曲线的顶点是该椭圆的焦点,设![]() 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线![]() 和
和![]() 与椭圆的交点分别为
与椭圆的交点分别为![]() 和
和![]() .
.
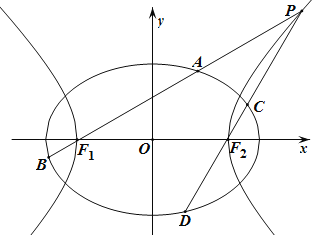
(Ⅰ)求椭圆和双曲线的标准方程;
(Ⅱ)设直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,证明
,证明![]() ;
;
(Ⅲ)是否存在常数![]() ,使得
,使得![]() 恒成立?若存在,求
恒成立?若存在,求![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与x、y轴分别交于点
与x、y轴分别交于点![]() 、
、![]() ,记以点
,记以点![]() 为圆心,半径为r的圆与三角形
为圆心,半径为r的圆与三角形![]() 的边的交点个数为M.对于下列说法:①当
的边的交点个数为M.对于下列说法:①当![]() 时,若
时,若![]() ,则
,则![]() ;②当
;②当![]() 时,若
时,若![]() ,则
,则![]() ;③当
;③当![]() 时,M不可能等于3;④M的值可以为0,1,2,3,4,5.其中正确的个数为( )
时,M不可能等于3;④M的值可以为0,1,2,3,4,5.其中正确的个数为( )
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过坐标原点的直线l与圆C:x2+y2﹣8x+12=0相交于不同的两点A,B.
(1)求线段AB的中点P的轨迹M的方程.
(2)是否存在实数k,使得直线l1:y=k(x﹣5)与曲线M有且仅有一个交点?若存在,求出k的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市100000名职业中学高三学生参加了一项综合技能测试,从中随机抽取100名学生的测试成绩,制作了以下的测试成绩![]() (满分是184分)的频率分布直方图.
(满分是184分)的频率分布直方图.
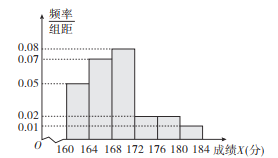
在频率分布直方图的分组中,以各组的区间中点值代表该组的各个值,测试成绩![]() 落入该区间的频率作为测试成绩取该区间中点值的概率.已知甲、乙两名学生的测试成绩分别为168分和170分.
落入该区间的频率作为测试成绩取该区间中点值的概率.已知甲、乙两名学生的测试成绩分别为168分和170分.
(1)求技能测试成绩![]() 的中位数
的中位数![]() ,对甲、乙的成绩作出客观的评价;
,对甲、乙的成绩作出客观的评价;
(2)若市教育局把这次技能测试看作技能大比武,且作出以下奖励规定:
给测试成绩![]() 者颁发奖金
者颁发奖金![]() 元,
元,
给测试成绩![]() 者颁发奖金元
者颁发奖金元![]() ,求
,求![]() ;
;
(3)若市教育局把这次技能看作是毕业过关测试,且作出以下规定:
当测试成绩![]() 时,统一交测试费和补测费300元;
时,统一交测试费和补测费300元;
当测试成绩![]() 时,统一交测试费100元;
时,统一交测试费100元;
当测试成绩![]() 时,免交测试费且颁发500元奖金.
时,免交测试费且颁发500元奖金.
若![]() ,据此统计:每个测试者平均最多应该交给教育局多少元?
,据此统计:每个测试者平均最多应该交给教育局多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com