过点(1,3)作直线l,若经过点(a,0)和(0,b),且a∈N*,b∈N*,则可作出的l的条数为( )
A.1
B.2
C.3
D.4
【答案】
分析:设出直线方程的截距式,把点(1,3)代入直线方程,变形得 3a=(a-1)b,检验a=1时的情况,当a≥2时,根据b=3+
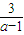
求a、b 的值.
解答:解:∵直线l过点(a,0)和(0,b),可设直线l的方程为:
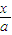
+
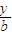
=1,
∵直线l过点(1,3),∴
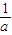
+

=1,即 3a=(a-1)b,又a∈N
*,b∈N
*,
∴当 a=1时,b=3,此时,直线和x轴垂直,和y轴无交点,直线不过(0,b),故a=1时不满足条件.
当 a≥2时,b=
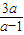
=3+
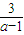
①,
当 a=2时,b=6,当 a=4时,b=4,
当a>4时,由①知,满足条件的正整数b不存在,
综上,满足条件的直线由2条,故选 B.
点评:本题考查直线的截距式方程的应用,把可作出的l的条数问题转化为求a、b 的值的个数问题,
体现了分类讨论和转化的数学思想.

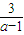 求a、b 的值.
求a、b 的值.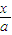 +
+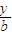 =1,
=1,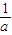 +
+ =1,即 3a=(a-1)b,又a∈N*,b∈N*,
=1,即 3a=(a-1)b,又a∈N*,b∈N*,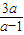 =3+
=3+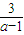 ①,
①,
