练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    如图，在正四棱柱ABCD－A1B1C1D1中AA1＝AB．点E、M分别为A1B1、C1C的中点，过点A1，B、M的平面交C1D1于N

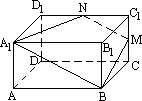
    (1)求证EM∥平面A1B1C1D1．

    (2)求二面角B－A1N－B1的正切值

    (3)设截面A1BMN把该正四棱柱截成的两个几何体的体积为V1，V2(V1＜V2)，求V1∶V2的值．

    答案：
    解析：

    　　(1)易证NMA1E

    　　∴四边形A1EMN为．

    　　∴ME∥A1N

    　　∴ME∥平面A1B1C1D1．

    　　(2)连B1N，易知B1N⊥A1N，B1N为BN在上底面射影．

    　　∴BN⊥A1N，则∠BNB1为所求，易知tanBNB1＝

    　　(3)延长A1N，B1C，BM，则三者交于一点P，且易知B1C1＝C1P．

    　　∵平面MNC1∥平面BA1B1

    　　∴几何体MNC1－BA1B1为棱台．＝()3＝，Vp－A1B1B＝×·2a·a·2a＝a3

    　　∴VNC1M－A1B1B＝×a3＝a3

    　　∴V1＝a3，V正面体＝2a3，V2＝(2－)a3＝a3，V1∶V2＝7∶17


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    精英家教网如图，在正四棱柱ABCD-A1B1C1D1中，已知AA1=4，AB=2，E是棱CC1上的一个动点．
    （Ⅰ）求证：BE∥平面AA1D1D；
    （Ⅱ）当CE=1时，求二面角B-ED-C的大小；
    （Ⅲ）当CE等于何值时，A1C⊥平面BDE．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    精英家教网如图，在正四棱柱ABCD-A′B′C′D′中（底面是正方形的直棱柱），侧棱AA′=
    		3
    ，AB=
    		2
    ，则二面角A′-BD-A的大小为（　　）
    A、30°B、45°
    C、60°D、90°

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2012•青岛一模）如图，在正四棱柱ABCD-A1B1C1D1中，AB=a，AA1=
    		2
    a    ，E为CC1的中点，AC∩BD=O．
    （Ⅰ） 证明：OE∥平面ABC1；
    （Ⅱ）证明：A1C⊥平面BDE．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    如图，在正四棱柱ABCD-A1B1C1D1中，AA1=A（x0，y0）AB=2，点E、M分别为A1B、C1C的中点．
    （Ⅰ）求证：EM∥平面A1B1C1D1；
    （Ⅱ）求几何体B-CME的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （2009•宜昌模拟）如图，在正四棱柱ABCD-A1B1C1D1 中，AB=BC=1，AA1=2．过顶点D1在空间作直线l，使l与直线AC和BC1所成的角都等于60°，这样的直线l最多可作（　　）

    查看答案和解析>>

    同步练习册答案