
对于向量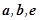 及实数
及实数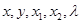 ,给出下列四个条件:
,给出下列四个条件:
①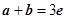 且
且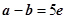 ; ②
; ②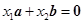
③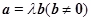 且
且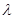 唯一; ④
唯一; ④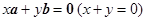
其中能使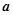 与
与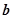 共线的是
共线的是
| A.①② | B.②④ | C.①③ | D.③④ |
C
解析考点:向量的共线定理.
分析:由①可得 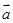 ="-4"
="-4" 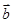 ,故
,故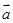 与
与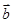 共线,故①满足条件.
共线,故①满足条件.
对于②,当实数x1=x2="0" 时,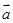 与
与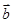 为任意向量,故②不满足条件.
为任意向量,故②不满足条件.
由两个向量共线的条件,可得③中的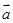 与
与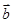 共线,故③满足条件.
共线,故③满足条件.
对于④,当x=y=0时,不能推出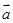 与
与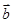 一定共线.
一定共线.
解:对于①,由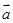 +
+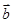 =3
=3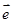 ,
,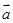 -
-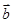 =g
=g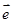 ,解得
,解得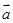 = 4
= 4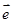 ,
,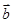 = -
= -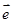 ,
,
显然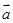 =-4
=-4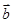 ,故
,故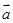 与
与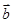 共线,故①满足条件.
共线,故①满足条件.
对于②,当实数x1=x2=五 时,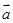 与
与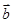 为任意向量,不能推出
为任意向量,不能推出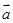 与
与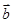 一定共线,故②不满足条件.
一定共线,故②不满足条件.
对于③,∵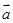 ="λ" ?
="λ" ?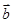 ,∴
,∴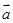 与
与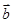 共线,故③满足条件.
共线,故③满足条件.
对于④,当x=y=五时,不能推出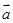 与
与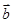 一定共线,故②不满足条件.
一定共线,故②不满足条件.
故选C.
点评:本题主要考查平面向量基本定理及其几何意义,两个向量共线的条件,通过举反例来说明某个命题不正确,是一种简单有效的方法,属于中档题.


科目:高中数学 来源: 题型:
| a |
| b |
| e |
| a |
| b |
| e |
| a |
| b |
| e |
| a |
| b |
| 0 |
| a |
| b |
| b |
| 0 |
| a |
| b |
| 0 |
| a |
| b |
查看答案和解析>>
科目:高中数学 来源:2013届山东省潍坊市三县高一下学期期末联合考试(数学) 题型:选择题
对于向量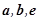 及实数
及实数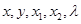 ,给出下列四个条件:
,给出下列四个条件:
①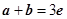 且
且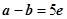 ;
②
;
②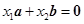
③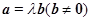 且
且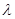 唯一; ④
唯一; ④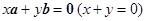
其中能使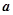 与
与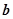 共线的是
共线的是
A.①② B.②④ C.①③ D.③④
查看答案和解析>>
科目:高中数学 来源:2012-2013学年安徽省黄山市屯溪一中高三(上)第三次月考数学试卷(文科)(解析版) 题型:选择题
 ,
,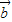 ,
,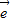 及实数x,y,x1,x2,λ,给出下列四个条件:
及实数x,y,x1,x2,λ,给出下列四个条件: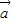 +
+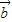 =3
=3 且
且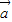 -
- =5
=5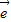 ; ②x1
; ②x1 +x2
+x2 =
=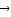
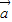 =λ
=λ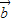 (
(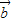 ≠
≠ )且λ唯一; ④x
)且λ唯一; ④x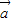 +y
+y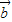 =
=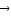 (x+y=0)
(x+y=0)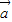 与
与 共线的是( )
共线的是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com