练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    函数y=ex-lnx的图象是（ ）
    A．
    B．
    C．
    D．
    【答案】分析：由于函数的定义域是（0，+∞），故可排除B选项，再借助于函数的导数就可判断出函数的极值个数，即可得到正确结论．
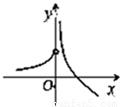
    解答：解：由题意知，函数y=ex-lnx的定义域为（0，+∞），可排除B；
    ∵y=ex-lnx，∴
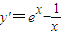
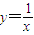
    而在区间（0，+∞）上，函数y=ex由1→+∞，函数由+∞→0，
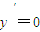
    故若令函数的导函数，则有且仅有一解，亦即函数y=ex-lnx只有一个极值点．
    故答案为A．
    点评：本题考查的是函数的图象与性质，函数的图象是函数的一种表达形式，形象地显示了函数的性质，为研究它的“形”的直观性常借助于函数的导数来完成．．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    函数y=ex+lnx的导函数y'=
    ex+
    1
    x
    ex+
    1
    x
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    函数y=ex+1的反函数是
    f-1（x）=lnx-1 （x＞0）
    f-1（x）=lnx-1 （x＞0）
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    函数y=ex-lnx的图象是（　　）

    查看答案和解析>>

    科目：高中数学 来源：2013年河南省南阳一中高考数学三模试卷（理科）（解析版） 题型：选择题

    函数y=ex-lnx的图象是（ ）
    A．
    B．
    C．
    D．

    查看答案和解析>>

    同步练习册答案