
 为数列
为数列 的前
的前 项和,对任意的
项和,对任意的 ,都有
,都有
 为常数,且
为常数,且 .
. 是等比数列;
是等比数列; 的公比
的公比 ,数列
,数列 满足
满足
 ,
,
 ,求数列
,求数列 的通项公式;
的通项公式; 的前
的前 项和
项和 .
.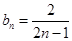 ;(3)
;(3)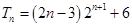
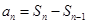
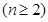 将
将 化简可得
化简可得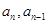 间的关系,根据等比数列的定义可证得数列
间的关系,根据等比数列的定义可证得数列 是等比数列。(2)属构造法求数列通项公式:因为
是等比数列。(2)属构造法求数列通项公式:因为
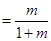 ,所以
,所以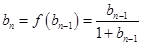 ,将其取倒数可推导出
,将其取倒数可推导出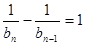 ,根据等差数列的定义可知
,根据等差数列的定义可知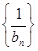 为等差数列,先求
为等差数列,先求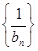 的通项公式,再求
的通项公式,再求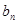 。(3)因为
。(3)因为 得通项公式为等差乘以等比数列所以应用错位相减法求数列的前
得通项公式为等差乘以等比数列所以应用错位相减法求数列的前 项和。将
项和。将 表示为各项的和,然后将上式两边同时乘以通项公式里边等比数列的公比,但应将第一位空出,然后两式相减即可。
表示为各项的和,然后将上式两边同时乘以通项公式里边等比数列的公比,但应将第一位空出,然后两式相减即可。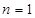 时,
时,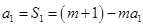 ,解得
,解得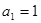 . 1分
. 1分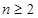 时,
时,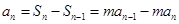 .即
.即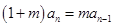 2分
2分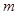 为常数,且
为常数,且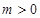 ,∴
,∴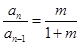
 . 3分
. 3分 是首项为1,公比为
是首项为1,公比为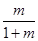 的等比数列. 4分
的等比数列. 4分
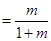 ,
,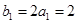 .
.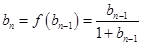 , ∴
, ∴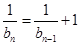 ,即
,即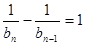
 . 7分
. 7分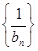 是首项为
是首项为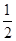 ,公差为1的等差数列. 8分
,公差为1的等差数列. 8分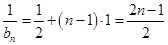 ,即
,即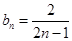 (
(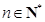 ). 9分
). 9分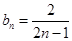 ,则
,则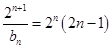 . 10分
. 10分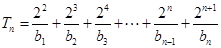 ,
,
 , ①
, ① 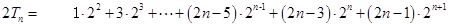 ②
②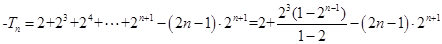 ,
,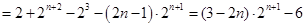
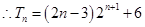 . 14分
. 14分

 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:高中数学 来源:不详 题型:解答题
 为等差数列,其公差d不为0,
为等差数列,其公差d不为0, 和
和 的等差中项为11,且
的等差中项为11,且 ,令
,令 ,数列
,数列 的前n项和为
的前n项和为 .
. 及
及 ;
; 成等比数列?若存在,求出所有的m,n的值;若不存在,请说明理由.
成等比数列?若存在,求出所有的m,n的值;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
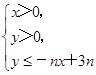 所表示的平面区域为Dn,记Dn内的整点个数为an(n∈N*)(整点即横坐标和纵坐标均为整数的点).
所表示的平面区域为Dn,记Dn内的整点个数为an(n∈N*)(整点即横坐标和纵坐标均为整数的点).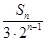 .若对于一切的正整数n,总有Tn≤m,求实数m的取值范围.
.若对于一切的正整数n,总有Tn≤m,求实数m的取值范围.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
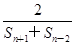 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
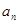 },Sn是数列{
},Sn是数列{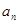 }的前n项和,S3=14,且al+8,3a2,a3+6依次成等差数列,则al·a3等于( )
}的前n项和,S3=14,且al+8,3a2,a3+6依次成等差数列,则al·a3等于( )| A.4 | B.9 | C.16 | D.25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com