
|
解: 过P作PE⊥BD于E, ∵ 平面ABD⊥平面CBD, ∴ PE⊥平面BCD, 过E作EF⊥CD, 连PF, 则PF⊥CD, ∴ ∠PFE为二面角P-CD-B的平面角. 设∠PFE=60° EF=a 在等腰△DBE中∠BDC=45°
又 ∵ ∠EFD=90°, ∴ DF=a, DE=
在Rt△PEF中, ∠PFE=60°, ∴ PF=2a, PE=
∴ BE= 在等腰Rt△ADB中,
AB=(
∴ 当P点分BA的比为 △PCD与△BCD所在平面所成的二面角为60°. |
| 作PE⊥BD于E, 过E作EF⊥CD于F, 连PF, 证明∠PFE为二面角P-CD-B的平面角. |


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:
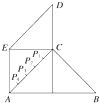
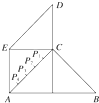 某县位于山区,居民的居住区域大致呈如右图所示的五边形,近似由一个正方形和两个等腰直角三角形组成,若AB=60km,AE=CD=30km,为了解决当地人民看电视难的问题,准备建一个电视转播台,理想方案是转播台距五边形各顶点的距离平方和最小,图中P1、P2、P3、P4是AC的五等分点,则转播台应建在( )
某县位于山区,居民的居住区域大致呈如右图所示的五边形,近似由一个正方形和两个等腰直角三角形组成,若AB=60km,AE=CD=30km,为了解决当地人民看电视难的问题,准备建一个电视转播台,理想方案是转播台距五边形各顶点的距离平方和最小,图中P1、P2、P3、P4是AC的五等分点,则转播台应建在( )查看答案和解析>>
科目:高中数学 来源: 题型:
某县位于山区,居民的居住区域大致呈如右图所示的五边形,近似由一个正方形和两个等腰直角三角形组成,若AB=60km,AE=CD=30km,为了解决当地人民看电视难的问题,准备建一个电视转播台,理想方案是转播台距五边形各顶点的距离平方和最小,图中P1、P2、P3、P4是AC的五等分点,则转播台应建在( )
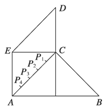
A.P1处 B.P2处
C.P3处 D.P4处
查看答案和解析>>
科目:高中数学 来源: 题型:
某县位于山区,居民的居住区域大致呈如右图所示的五边形,近似由一个正方形和两个等腰直角三角形组成,若AB=60km,AE=CD=30km,为了解决当地人民看电视难的问题,准备建一个电视转播台,理想方案是转播台距五边形各顶点的距离平方和最小,图中P1、P2、P3、P4是AC的五等分点,则转播台应建在( )
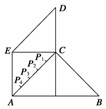
A.P1处 B.P2处
C.P3处 D.P4处
查看答案和解析>>
科目:高中数学 来源:2013届福建省高二期末考试文科数学试卷(解析版) 题型:选择题
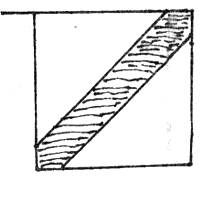
如图所示,在边长为10cm的正方形中挖去直角边长为8cm的两个等腰直角三角形,现有均匀的粒子散落在正方形中,则粒子落在中间带形区域的概率是( )
A. 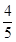 B.
B.
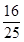
C. 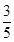 D.
D.
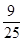
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.P1处 | B.P2处 | C.P3处 | D.P4处 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com