
设函数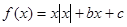 ,给出以下四个命题:①当c=0时,有
,给出以下四个命题:①当c=0时,有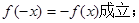 ②当b=0,c>0时,方程
②当b=0,c>0时,方程 ③函数
③函数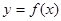 的图象关于点(0,c)对称 ④当x>0时;函数
的图象关于点(0,c)对称 ④当x>0时;函数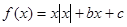 ,
, 。其中正确的命题的序号是_________。
。其中正确的命题的序号是_________。
1.2.3
【解析】
试题分析::①c=0,f(x)=x|x|+bx,f(-x)=-x|-x|+b(-x)=-f(x),故①正确
②b=0,c>0,f(x)=x|x|+c= x2+c,x≥0
-x2+c,x<0
令f(x)=0可得x=-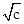 ,故②正确
,故②正确
③设函数y=f(x)上的任意一点M(x,y)关于点(0,c)对称的点N(x′,y′),则x=-x’,y=2c-y’代入y=f(x)可得2c-y′=-x′|-x′|-bx′+c⇒y′=x′|x′|+bx′+c故③正确
④当x>0时;函数 ,是开口向上的二次函数,那么由于对称轴的正负不定,因此
,是开口向上的二次函数,那么由于对称轴的正负不定,因此 错误,应该是不确定的。故填写1.2.3
错误,应该是不确定的。故填写1.2.3
考点:本试题主要考查了函数的奇偶性、对称性(中心对称的证明)及函数图象在解题中的运用,要求考生熟练掌握函数的性质,并能灵活运用性质求解.
点评:解决该试题的关键是熟练的运用函数的奇偶性和对称性来分析和解决问题,另外对于绝对值问题,常常去掉绝对值来分析得到结论。


科目:高中数学 来源:2007届深圳市龙华中英文实验学校理科数学测试题 题型:022
设函数![]() ,给出以下四个论断:①
,给出以下四个论断:①![]() 的周期为π;②
的周期为π;②![]() 在区间(-
在区间(-![]() ,0)上是增函数;?③
,0)上是增函数;?③![]() 的图象关于点(
的图象关于点(![]() ,0)对称;?④
,0)对称;?④![]() 的图象关于直线
的图象关于直线![]() 对称.?以其中两个论断作为条件,另两个论断作为结论,写出你认为正确的一个命题:?________
对称.?以其中两个论断作为条件,另两个论断作为结论,写出你认为正确的一个命题:?________![]() ________(只需将命题的序号填在横线上).
________(只需将命题的序号填在横线上).
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省梅州市高一(上)第二次质检数学试卷(解析版) 题型:填空题
 ,给出以下四个论断:
,给出以下四个论断: 对称;
对称;  对称;
对称;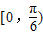 上是增函数.
上是增函数.查看答案和解析>>
科目:高中数学 来源:2011年江苏省高一上学期期末考试数学试卷 题型:填空题
设函数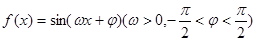 ,给出以下四个论断:
,给出以下四个论断:
①它的图象关于直线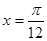 对称; ③它的最小正周期是
对称; ③它的最小正周期是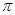 ;
;
②它的图象关于点( ,0)对称;④在区间[
,0)对称;④在区间[ ]上是增函数.
]上是增函数.
以其中两个论断作为条件,余下论断作为结论,写出一个正确的命题:
条件_ ▲ _ ,结论_▲ (填序号)
查看答案和解析>>
科目:高中数学 来源:2014届江苏省高一12月月考数学试卷 题型:填空题
设函数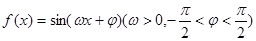 ,给出以下四个论断:
,给出以下四个论断:
①它的图象关于直线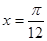 对称; ③它的最小正周期是
对称; ③它的最小正周期是 ;
;
②它的图象关于点(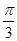 ,0)对称;
④在区间[
,0)对称;
④在区间[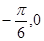 ]上是增函数.
]上是增函数.
以其中两个论断作为条件,余下论断作为结论,写出一个正确的命题:
条件_ ▲ _ ,结论_ ▲ (填序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
设函数![]() ,给出以下四个论断:
,给出以下四个论断:
①它的图象关于直线![]() 对称; ③它的最小正周期是
对称; ③它的最小正周期是![]() ;
;
②它的图象关于点(![]() ,0)对称;④在区间[
,0)对称;④在区间[![]() ]上是增函数.
]上是增函数.
以其中两个论断作为条件,余下论断作为结论,写出一个正确的命题:
条件_ ▲ _ ,结论_▲ (填序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com