
| A.25,17,8 | B.25,16,9 | C.26,16,8 | D.24,17,9 |
 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源:不详 题型:单选题
| A.45,44 | B.45,47 | C.42,46 | D.42,47 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
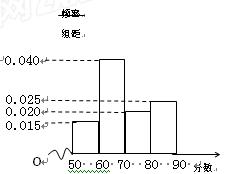
 分配相应的低息贷款金额,其评估标准和贷款金额如下表:
分配相应的低息贷款金额,其评估标准和贷款金额如下表:| 评估得分 | [50,60) | [60,70) | [70,80) | [80,90] |
| 评定类型 | 不合格 | 合格 | 良好 | 优秀 |
| 贷款金额(万元) | 0 | 200 | 400 | 800 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

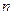 个人,已知从“支持”态度的人
个人,已知从“支持”态度的人 中抽取了45人
中抽取了45人 ,求
,求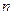 的值;
的值; “不支持”态度的人中,用分层抽样的方法抽取5人看成一
“不支持”态度的人中,用分层抽样的方法抽取5人看成一 个总体,从这5人中任意选取2人,求至少有
个总体,从这5人中任意选取2人,求至少有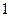 人20岁以下的概率;
人20岁以下的概率;查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
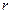 的值及对应的临界值
的值及对应的临界值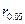 后,下列说法正确的是 ( )
后,下列说法正确的是 ( )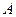 、如果
、如果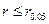 ,那么接受统计假设;
,那么接受统计假设; 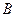 、如果
、如果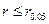 ,那么拒绝统计假设;
,那么拒绝统计假设;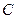 、如果
、如果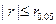 ,那么接受统计假设;
,那么接受统计假设; 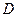 、如果
、如果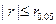 ,那么拒绝统计假设;
,那么拒绝统计假设; 查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| | 优秀 | 不优秀 | 合计 |
| 甲班 | 10 | 35 | 45 |
| 乙班 | 7 | 38 | 45 |
| 合计 | 17 | 73 | 90 |
A.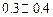 | B.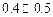 | C.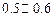 | D.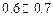 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com