
(本题共12分)
据统计某种汽车的最高车速为120千米∕时,在匀速行驶时每小时的耗油量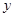 (升)与
(升)与
行驶速度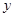 (千米∕时)之间有如下函数关系:
(千米∕时)之间有如下函数关系: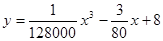 。已知甲、乙
。已知甲、乙
两地相距100千米。
(I)若汽车以40千米∕时的速度匀速行驶,则从甲地到乙地需耗油多少升?
(II)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
(I)汽车以40千米∕时的速度匀速行驶,从甲地到乙地需耗油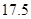 升;
升;
(II)当汽车以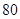 千米∕时的速度行驶时,从甲地到乙地耗油最少,最少为
千米∕时的速度行驶时,从甲地到乙地耗油最少,最少为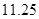 升。
升。
【解析】本试题主要考查了函数在实际问题中的运用。利用已知条件,表示函数关系式,然后借助于函数的性质得到最值。
(1)当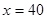 时,汽车从甲地到乙地行驶了
时,汽车从甲地到乙地行驶了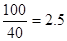 (小时),
(小时),
需蚝油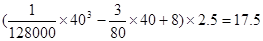 (升)。
(升)。
(2)当汽车的行驶速度为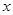 千米∕时时,从甲地到乙地需行驶
千米∕时时,从甲地到乙地需行驶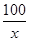 小时.设耗油量为
小时.设耗油量为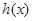 升,依题意,得
升,依题意,得 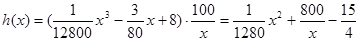
其中,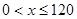
借助于导数的思想求解最值。
(I)当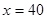 时,汽车从甲地到乙地行驶了
时,汽车从甲地到乙地行驶了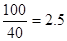 (小时),
(小时),
需蚝油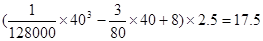 (升)。
(升)。
所以,汽车以40千米∕时的速度匀速行驶,从甲地到乙地需耗油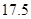 升…4分.
升…4分.
(II)当汽车的行驶速度为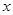 千米∕时时,从甲地到乙地需行驶
千米∕时时,从甲地到乙地需行驶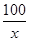 小时.设耗油量为
小时.设耗油量为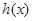 升,依题意,得
升,依题意,得 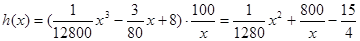
其中,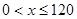 .………………………………………………………… 7分
.………………………………………………………… 7分
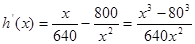
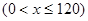 .
.
令 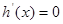 ,得
,得 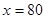 .
.
因为当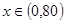 时,
时,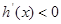 ,
,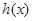 是减函数;当
是减函数;当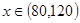 时,
时,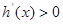 ,
,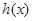 是增函数,所以当
是增函数,所以当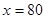 时,
时,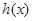 取得最小值
取得最小值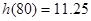 .
.
所以当汽车以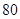 千米∕时的速度行驶时,从甲地到乙地耗油最少,
千米∕时的速度行驶时,从甲地到乙地耗油最少,
最少为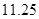 升。………………………………………………………………
12分
升。………………………………………………………………
12分


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2013届山东冠县武训高中高二下第三次模块考试理科数学试题(解析版) 题型:解答题
(本题共12分)据统计某种汽车的最高车速为120千米∕时,在匀速行驶时每小时的耗油量 (升)与行驶速度
(升)与行驶速度 (千米∕时)之间有如下函数关系:
(千米∕时)之间有如下函数关系: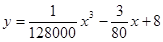 。已知甲、乙两地相距100千米。
。已知甲、乙两地相距100千米。
(I)若汽车以40千米∕时的速度匀速行驶,则从甲地到乙地需耗油多少升?
(II)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com