
写出由下列各组命题构成的“p或q”、“p且q”、“ p”形式的复合命题,并判断真假.
p”形式的复合命题,并判断真假.
(1)p:1是质数;q:1是方程x2+2x-3=0的根;
(2)p:平行四边形的对角线相等;q:平行四边形的对角线互相垂直;
(3)p:0∈∅;q:{x|x2-3x-5<0}⊆R;
(4)p:5≤5;q:27不是质数.
(1)p为假命题,q为真命题.
p或q:1是质数或是方程x2+2x-3=0的根.真命题.
p且q:1既是质数又是方程x2+2x-3=0的根.假命题.
 p:1不是质数.真命题.
p:1不是质数.真命题.
(2)p为假命题,q为假命题.
p或q:平行四边形的对角线相等或互相垂直.假命题.
p且q:平行四边形的对角线相等且互相垂直.假命题.
 p:有些平行四边形的对角线不相等.真命题.
p:有些平行四边形的对角线不相等.真命题.
(3)∵0∉∅,∴p为假命题,
又∵x2-3x-5<0,∴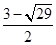 <x<
<x<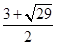 ,
,
∴{x|x2-3x-5<0}
=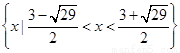 ⊆R成立.
⊆R成立.
∴q为真命题.
∴p或q:0∈∅或{x|x2-3x-5<0}⊆R,真命题,
p且q:0∈∅且{x|x2-3x-5<0}⊆R,假命题,
 p:0∉∅,真命题.
p:0∉∅,真命题.
(4)显然p:5≤5为真命题,q:27不是质数为真命题,∴p或q:5≤5或27不是质数,真命题,
p且q:5≤5且27不是质数,真命题,
 p:5>5,假命题.
p:5>5,假命题.
【解析】主要考查简单的逻辑联结词的含义。
解:(1)p为假命题,q为真命题.
p或q:1是质数或是方程x2+2x-3=0的根.真命题.
p且q:1既是质数又是方程x2+2x-3=0的根.假命题.
 p:1不是质数.真命题.
p:1不是质数.真命题.
(2)p为假命题,q为假命题.
p或q:平行四边形的对角线相等或互相垂直.假命题.
p且q:平行四边形的对角线相等且互相垂直.假命题.
 p:有些平行四边形的对角线不相等.真命题.
p:有些平行四边形的对角线不相等.真命题.
(3)∵0∉∅,∴p为假命题,
又∵x2-3x-5<0,∴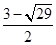 <x<
<x<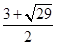 ,
,
∴{x|x2-3x-5<0}
=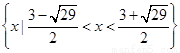 ⊆R成立.
⊆R成立.
∴q为真命题.
∴p或q:0∈∅或{x|x2-3x-5<0}⊆R,真命题,
p且q:0∈∅且{x|x2-3x-5<0}⊆R,假命题,
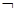 p:0∉∅,真命题.
p:0∉∅,真命题.
(4)显然p:5≤5为真命题,q:27不是质数为真命题,∴p或q:5≤5或27不是质数,真命题,
p且q:5≤5且27不是质数,真命题,
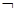 p:5>5,假命题.
p:5>5,假命题.


 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)p:平行四边形的对角线相等;q:平行四边形的对角线互相平分.
(2)p:方程x2-16=0的两根的符号不同;q:方程x2-16=0的两根的绝对值相等.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com